Inscription / Connexion Nouveau Sujet
developpement limite ( fonction d'une seule variable)
SALUT A TOUS, AIDER MOI SVP. ON ME DEMANDE D'ETUDIER LA BRANCHE INFINIE POUR XTENDANT VERS -L'INFINI DE LA COURBE DE L'EQUATION:
Y=RACINE Nième DE 3 DE(X AU CUBE+X AU CARRE+1)-RACINE Nième DE 2 DE (X AU CARRE-X-1). JE NE SAIS PAS SIL FAUT FAIRE UN DEVELOPPEMENT LIMITE AVANT DE CALCULER LA LIMITE ET SI OUI COMMENT FAIRE?
Y=3 ((X)3+X²+1) - ²
((X)3+X²+1) - ² (X²-X-1)
(X²-X-1)
vous avez raison, excusez donc. mais comprenez moi car je suis nouveau a faire ce genre de chose alors je ne sais pas comment ça marche.
ben déjà évite d'écrire en MAJUSCULES ! Ca donne l'impression que tu cries ou que tu hurles (enfin c'est une convention typographique que j'interprète de cette manière...).
Ensuite, pour "racine troisième ", on dit "racine cubique" et pour "racine deuxième" "racine carrée".
Ce sont les deux seules racines nième qui ont une appellation propre. La fonction racine nième, elle, est la fonction
Enfin, un développement limité te permettra de calculer la limite puisque tu vois bien que là tu as une forme indéterminée. Pour le reste ton cours doit te donner la méthode...
et juste pour préciser on a la convention puisque
la fonction racine nième est donc celle que j'ai définie ci-dessus mais sur seulement.
Bon on va pas s'étendre là-dessus. Je te laisse reprendre...
une autre règle du forum : quand on ouvre un topic on montre ce qu'on a fait, on pose des questions...
mais on évite de laisser le topic à l'abandon tant que le problème n'est pas résolu !
Donc j'accepterai tes remerciements quand tu auras compris et résolu ton problème !
On conjecture en - une asymptote oblique d'équation y=2x.
une asymptote oblique d'équation y=2x.
Essaye de trouver par le calcul que
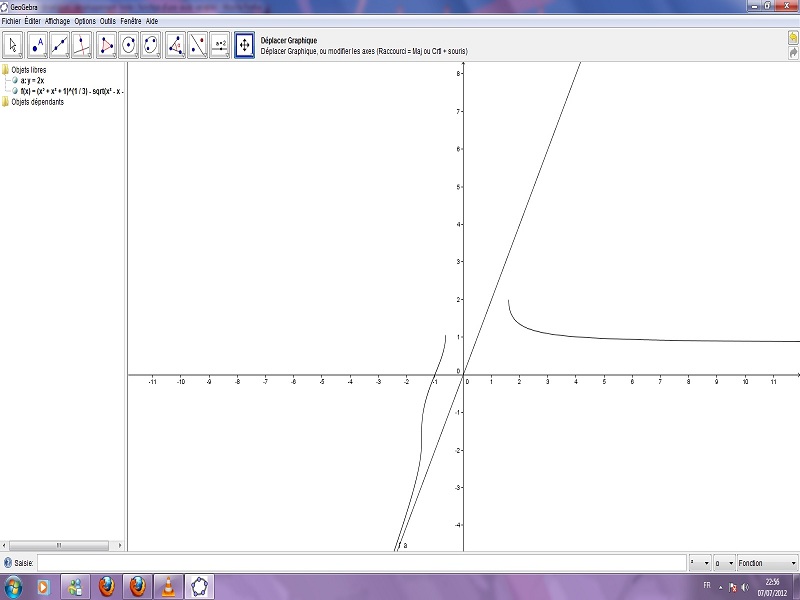
lorsque j'ai lu vos message j'ai pu transformé la fonction en procédant par un développement limité de la fonction.
ensuite j'ai calculé la limite de la fonction que j'ai trouvé en moins infini et j'ai trouvé 1.
j'ai donc conclure que l'équation y admettait une branche infinie.
wolfram confirme les dires d'alb donc je me suis à peine planter dans mes calculs...
Il faut trouver que
la limite n'est pas 1 du tout !
non, ça n'a rien à voir, il faut que pour avoir une asymptote oblique, ce qui me semble bien être le cas ici !!
NON ! La limite en - est -
est - donc on peut avoir une branche parabolique, une branche infinie, une asymptope oblique... On en sait rien à priori ! C'est bien le calcul du développement limité de f à l'ordre 2 ou 3 (à toi devoir) qui te donne
donc on peut avoir une branche parabolique, une branche infinie, une asymptope oblique... On en sait rien à priori ! C'est bien le calcul du développement limité de f à l'ordre 2 ou 3 (à toi devoir) qui te donne
1) l'équation de l'asymptote (ici y=2x -1/6)
2) la position de cette asymptote par rapport à ta courbe (ici -53/72x > 0 au voisinage de - donc ta courbe est au-dessus de son asymptote...)
donc ta courbe est au-dessus de son asymptote...)
Mais il faut que tu fasses les calculs par toi-même, calculs que je n'ai pas détaillés ici !
lorsque je fais mes calcul, si je ne me trompe pas bien sur, il me semble que Alexique s'est trompé dans les calculs. car ne utilisant le développement limité, si je ne me trompe aussi on trouve :
f(x)= 1 + (-1/6)X + 13/12X + 5/6X + 0(X²)
la limite de cette fonction lorsque x -
- est +
est + il y a donc possibilité qu'il ait une branche parabolique, une asymptote ou une branche infinie. mais pour determiner les branche infinie, j'ai donc calculé la limite lorsque x
il y a donc possibilité qu'il ait une branche parabolique, une asymptote ou une branche infinie. mais pour determiner les branche infinie, j'ai donc calculé la limite lorsque x -
- de f(x)/x. ce qui n'est pas égale a
de f(x)/x. ce qui n'est pas égale a 
 . j'ai donc dis qu'il n'y a pas de branche infinie. or dans l'exercie en question on me demande d'étudier la branche infinie. qu'en dites-vous?
. j'ai donc dis qu'il n'y a pas de branche infinie. or dans l'exercie en question on me demande d'étudier la branche infinie. qu'en dites-vous?
J'en dis que si tu sais que ce qu'est wolfram (à savoir un logiciel de calcul formel en ligne), le dernier résultat que j'ai donné est correcte puisque je l'ai obtenu avec wolfram donc le tien est faux d'une part, et d'autre part,
si f(x)/x tend vers un réel mettons a, et que f(x) - ax tend vers un reel mettons b, alors y=ax+b est asymptote oblique à la courbe en - (cf post d'alkan :
(cf post d'alkan : ).
bon essayons :
et pour l'ordonnée à l'origine le b c'est casse-pieds (essaye de trouver la limite de f(x)-2x) et pour la position de l'asymptote par rapport à la courbe, j'en parle même pas ! Donc DL ! Toujours pour x<0
d'où le résultat
en utilisant : et en tronquant au fur à mesure des calculs...
Mais ça il faut que tu saches le faire toi-même !!
Donc . Mon message de 11h37 te donne le reste.
Je préférerais que tu me dises que tu comprends tout ça et que tu m'insultes plutôt que tu ne comprennes rien du tout et que tu me remercies...
Si il y a des maladresses, il faut me les signaler...
J'en dis que tu es un tantinet têtu.
Tu dois démontrer que la droite d'équation y=2x-1/6 est une asymptote au voisinage de -inf. Si tu n'es pas convaincu voici les résultats avec un autre logiciel.
1/ Méthode 1 qui paraît la plus adaptée
g(x):=-(-x^3-x^2-1)^(1/3)-sqrt(x^2-x-1)
somme(simplifier(op(series(g(x),x=-inf,2))))
latex(ans())
et on obtient:
2/ Méthode 2
limite(g(x)/x,x,-inf) renvoie 2
limite(g(x)-2x,x,-inf) renvoie -1/6
voici la formule que j'ai utilisé pour faire le développement limité: (1+z) =(z-n+1)zn/nfactoriel +0(zn). en l'appliquant a cette fonction je ne comprend comment vous aboutissez a votre resultat. je sais que ça peut vous faire mal mais c'est la vérité.
=(z-n+1)zn/nfactoriel +0(zn). en l'appliquant a cette fonction je ne comprend comment vous aboutissez a votre resultat. je sais que ça peut vous faire mal mais c'est la vérité.
vous faites ces démonstrations avec des logiciels, mais je le fais avec le bic alors peut etre que la formule que j'utilise est différentes des vôtres. j'utilise ce que j'ai appris à l'école.
x est censé tendre vers - donc on peut déjà le supposer négatif ! J'en avais besoin à cause de cette histoire de valeur absolue car
donc on peut déjà le supposer négatif ! J'en avais besoin à cause de cette histoire de valeur absolue car . Ici la fonction racine cubique est définie sur R tout entier. Sur R+ c'est
et sur R- son opposé car c'est une fonction impaire (fonction racine nième est définie sur R si n impaire, sur R+ seulement sinon...).
Quant à ta formule, elle me parait très bizarre si ce n'est fausse.
Par contre, ton cours dit peut-être ceci :
ce que j'ai employé avec et n=3.
Enfin, tu es effectivement très têtu ! J'ai fait les calculs à la main, je les ai rédigés en Latex, j'ai appris à faire ça cette année et n'importe quel étudiant en L1 doit savoir faire ça rapidement sans erreur. Les logiciels donnent des résultats justes et aident à voir ses propres erreurs, c'est pourquoi à moins d'être stupide, tu ne peux pas sérieusement penser que ton résultat est correct ! La méthode QUAND ELLE EST BIEN APPLIQUEE mène toujours à un bon résultat (la machine sans exception, l'homme avec quelques unes...).
Enfin, la vérité ne m'a jamais fait mal (c'est certainement pour la rechercher de la vérité à l'état pur que j'ai choisi d'étudier les mathématiques de même que bon nombre de personnes sur ce forum je pense) et sans aucun orgueil ou mépris de ma part, je sais reconnaitre quand j'ai raison ou tort (je me suis moi-même trompé dans ce topic et j'ai immédiatement reconnu mes torts !). Il serait judicieux que tu en fasses de même puisqu'on "apprend de ses erreurs".
Si d'autres personnes ont plus de patience et de pédagogie que moi, qu'elles n'hésitent pas à entrer dans le débat et à prendre ma place !
ho mon Dieu,c'est comme si j'était voilé. je viens juste de m'apercevoir que je me trompais au moment même où je devrais remplacer la fonction posée. en tout cas merci beaucoup tu ma permis de voir clair
Révélation tardive ! mais mieux vaut tard que jamais 
Cala dit tu devrais corriger ta formule pour développer (1+x)^a

 0
0 0
0
 analyse en post-bac
analyse en post-bac