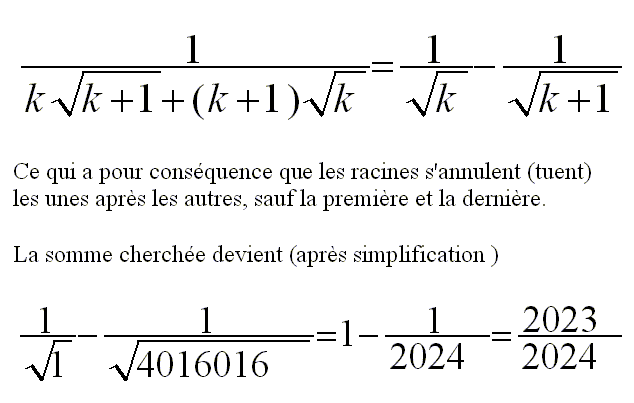Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques EnigmesTentez votre chance à l'énigme du jour pour gagner le concours mensuel... 2 *Les énigmes faciles [tout]Lister tous les topics de mathématiques
Niveau 2 *
Partager :

ENIGMA 16: Tue-Racines**

Posté par
monrow Posteur d'énigmes 14-02-08 à 02:40

Bonjour

je me permet de poster une très petite énigme astucieuse plutôt orientée côté maths (pas beaucoup en fait )

\Large\rm \Bigsum_{k=1}^{4016015}\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} peut s'exprimer beaucoup beaucoup plus gentiment sous la forme de \Large \frac{a}{b} avec a et b deux entiers naturels.

Pouvez vous trouver a et b?


L'usage d'une calculatrice ou d'un programme est interdit ! Une démarche bien claire est nécessaire pour avoir son smiley

ENIGMA 16: Tue-Racines

Bon calcul !

* correction énoncé le 14/02 à 09:28 *

Posté par
Nofutur2re : ENIGMA 16: Tue-Racines** 14-02-08 à 09:36

gagnéEn multipliant numérateur et dénominateur de la fraction par le conjugué, on obtient :
((k+1) k - k (k+1))/(k*(k+1)), soit 1/k - 1/ (k+1).
En sommant on obtient 1/1 - 1/ (4016105+1).
Ici, j'ai supposé qu'il y avait une erreur d'énoncé et que la borne supérieure était 4016015 au lieu de 4016105.
On obtient donc :
1-1/2004 = 2003/2004
a=2003 et b=2004.

Posté par
master_ochre : ENIGMA 16: Tue-Racines** 14-02-08 à 11:21

gagnéBonjour

on a 1/(k(k+1)+(k+1)k)

= (1+k-k)/[k . (k+1) .(k + (k+1))]

= ([(1+k)]²-[k]²)/[k . (k+1) .(k + (k+1))]

=  ((k+1) - k)/[k . (k+1)]

= 1/k   -   1/(k+1)

par élimination terme à terme notre somme S s'écrira:
S=1-1/(4016015+1)=1-1/4016016

or ona 4016016 = 4.106+16.103+16 = (2.103)² + 2x4x2.103+4² (produit remarquable) ==> 4016016 = (2.103+4)² = 2004².

==> S= 1-1/2004 = 2003/2004

d'ou a=2003  ,  b=2004

merci pour l'énigme .

Posté par
rogerdTue racines 14-02-08 à 11:41

gagnéMerci à Monrow pour cette avalanche de jolies énigmes!

En multipliant haut et bas par la quantité conjuguée
\frac1{k\sqrt{k+1}+(k+1)\sqrt k}=\frac{(k+1)\sqrt k-k\sqrt{k+1}}{(k+1)^2k-k^2(k+1)}=\frac{(k+1)\sqrt k-k\sqrt{k+1}}{k(k+1)}=\frac{\sqrt k}k-\frac{\sqrt{k+1}}{k+1}

En sommant de 1 à 4016015, les termes se télescopent et il ne reste que
1-\frac{sqrt{4016016}}{4016016}=1-\frac1{\sqrt{4016016}}.
En factorisant dans 4016016 le maximum de carrés, on voit que c'est le carré de 2.2.3.167 (avec un peu de tâtonnements pour 167).
La somme est donc égale à 1-\frac1{2004}=\frac{2003}{2004}

Donc a=2003 et b=2004.

Posté par
Flo08re : ENIGMA 16: Tue-Racines** 14-02-08 à 11:45

gagnéBonjour,


Je commence par multiplier le numérateur et le dénominateur par     k\sqrt{k+1}-(k+1)\sqrt{k}    pour éliminer les racines carrées du dénominateur. Après avoir simplifié l'expression, je constate que tous les termes intermédiaires de la somme s'annulent :


\Large\rm \Bigsum_{k=1}^{4016015}\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} = \Large\rm \Bigsum_{k=1}^{4016015} \frac{k\sqrt{k+1}-(k+1)\sqrt{k}}{k^2(k+1)-k(k+1)^2} = \Large\rm \Bigsum_{k=1}^{4016015} \frac{k\sqrt{k+1}-(k+1)\sqrt{k}}{k^3+k^2-k^3-2k^2-k}


\Large = \rm \Bigsum_{k=1}^{4016015} \frac{k\sqrt{k+1}-(k+1)\sqrt{k}}{-k(k+1)} = \Large\rm \Bigsum_{k=1}^{4016015} (\frac{\sqrt{k}}{k} - \frac{\sqrt{k+1}}{k+1}) = \frac{\sqrt{1}}{1} - \frac{\sqrt{4016016}}{4016016}


\Large = 1 - \frac{\sqrt{4016016}}{4016016} = \frac{4016016-\sqrt{4016016}}{4016016} = \frac{4016016-2004}{4016016} = \frac{2003}{2004}


\blue \fbox{\Large\rm \Bigsum_{k=1}^{4016015}\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} = \frac{2003}{2004}}

Posté par
simon92re : ENIGMA 16: Tue-Racines** 14-02-08 à 17:20

gagnéSalut,
Je penseu que la partie en fonction de k que l'on somme vaut \frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}.
En sommant, on remarque que cela donne 1-\frac{1}{\sqrt{4016015+1}}
Soit, 1-\frac{1}{2004}=\frac{2003}{2004}

Posté par
veledare : ENIGMA 16: Tue-Racines** 14-02-08 à 19:38

gagnébonjour,
je suis partie ce matin avec la première version: problème impossible
sinon c'est simplement le principe des dominos
ukle terme général de la somme s'écrit( 1/k)-(1/k+1) expression obtenue en multipliant numérateur et dénominateur par  [k(k+1)-(k+1)k]
\bigsum_{k=1}^{4016015}u_k=1-1/4016016 ( principe des dominos les termes s'éliminent deux à deux sauf le premier et le dernier)
or 4016016=2004²
donc la somme est égale à 1-1/2004=2003/2004=a/b

merci d'avoir corrigé l'énoncé

Posté par
plumemeteorere : ENIGMA 16: Tue-Racines** 14-02-08 à 23:26

gagnébonsoir
la somme est 2003/2004
la somme des n premiers termes est [V(n+1)-1]/V(n+1)
c'est vrai pour n = 1
1/(V2+2) = (V2-1)/V2 car les produits en croix V2 et (V2-1)(V2+2) = 2+2V2-V2-2 = V2 sont égaux
si c'est vrai pour n-1, c'est vrai pour n
la somme des n premiers termes est (Vn-1)/Vn + 1/[nV(n+1)+(n+1)Vn]; cette addition donne une fraction A
le numérateur de A est (Vn - 1)[nV(n+1) + (n+1)Vn] + Vn
= nVnV(n+1) + n(n+1) - nV(n+1) - (n+1)Vn + Vn
= nVnV(n+1) + n² + n - nV(n+1) - nVn
le dénominateur de A = Vn[nV(n+1) + (n+1)Vn]
= nVnV(n+1) + n(n+1) = nVnV(n+1) + n² + n
A = [(nVnV(n+1) + n² + n) / (nVnV(n+1) + n² + n)] - [(nV(n+1) + nVn) / (nVnV(n+1) + n² + n)]
or (nV(n+1) + nVn) / (nVnV(n+1) + n² + n) = (V(n+1) + Vn) / (VnV(n+1) + n + 1) = 1/V(n+1) car les produits en croix sont égaux
V(n+1)(V(n+1) + Vn) = n+1 + VnV(n+1) = VnV(n+1) + n + 1
donc A = 1 - 1/V(n+1) = [V(n+1)-1]/V(n+1) cqfd

Posté par
chocwomantue racines 15-02-08 à 09:24

gagnébonjour
en factorisant le dénominateur du terme général de la somme par k* (k+1) puis en multipliant numérateur et dénominateur par (k+(k+1)),le terme général est égal à
((k+1)-k)/(k*(k+1)), ceci étant aussi égal à
(1/k)-(1/(k+1)).
en sommant de k=1 à k=4016015
on obtient 1-1/4016016
c'est à dire 1-1/2004
ce qui vaut 2003/2004.
Mon résultat est donc 2003/2004

Posté par
ITMETICre : ENIGMA 16: Tue-Racines** 15-02-08 à 09:41

gagnéExprimons le terme général d'une façon plus simple

Commençons par factoriser le numérateur en mettant ((k(k+1))en facteur commun

k(k+1)+(k+1)k=((k(k+1))((k+1)+k)

Puis multiplions dénominateur et numérateur par (k+1)-k, quantité conjuguée de (k+1)+k

Le numérateur devient (k+1)-k
alors que le dénominateur devient ((k(k+1)

Il n'y a plus qu'à séparer les deux termes et à simplifier pour obtenir
1/k-1/(k+1)

Quand on calculera la somme les termes se simplifierons deux à deux et il ne restera que
1-1/4016016=1-1/2004=2003/2004

Posté par
freniclere : ENIGMA 16: Tue-Racines** 15-02-08 à 12:51

gagnéBonjour monrow

On vérifie facilement que :

3$ \frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}}=\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}

La somme est donc "télescopique" et vaut

3$ 1 - \frac{1}{\sqrt{4016016}} = 1 - \frac{1}{2004} = \frac{2003}{2004}

Cordialement
Frenicle

Posté par
infophilere : ENIGMA 16: Tue-Racines** 15-02-08 à 13:37

gagnéBonjour

3$ \rm \frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}}=\frac{1}{\sqrt{k}\sqrt{k}\sqrt{k+1}+\sqrt{k+1}\sqrt{k+1}\sqrt{k}}=\frac{1}{\sqrt{k}\sqrt{k+1}(\sqrt{k+1}+\sqrt{k})}=\frac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k}\sqrt{k+1}}=\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}

On a donc une somme télescopique, et comme de par hasard 4016015 + 1 = 2004² donc :

La somme s'écrit 3$ \rm S=1-\frac{1}{2004}=\frac{2003}{2004}

Sauf erreur

Posté par
davidhre : ENIGMA 16: Tue-Racines** 15-02-08 à 14:20

gagnéBonjour,

Je résume un peu les calculs
\frac{1}{\sqrt{k}\sqrt{k+1}(\sqrt{k}+\sqrt{k+1})}=\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}

Donc la somme est égale à 1-1/2004

Donc a=2003 et b=2004

Posté par
geo3re : ENIGMA 16: Tue-Racines** 15-02-08 à 16:24

gagnéBonjour

5$\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} = \frac{1}{(k+1)\sqrt{k}+k)\sqrt{k+1}}=

5$\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{(k+1)^2k-k^2 (k+1)}=

en multipliant par le conjugué

5$\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{(k+1)k(k+1-k)}= \frac{\sqrt{k}}{k}-\frac{\sqrt{k+1}}{k+1}=\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}

5$\sum_1^{4016015}(\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}})=1-\frac{1}{\sqrt{4016016}}=1-\frac{1}{2004}=

5$\red=\frac{2003}{2004}

Posté par
lune et etoileenigma16:Tue-Racines 16-02-08 à 17:22

perdusoit :Ak=1/(kV(k+1) +(k+1)Vk en multipliant numérateur et dénominateur par le conjugué du dénominateur on obtient Ak =(kV(k+1) -(k+1)Vk) /-k(k+1)ou encore Ak =Vk/k -V(k+1)/k     (V désigne racine carrée)
la somme des Ak ,k variant de 1 à 4016015 est égale à V1/1 -V4016016/4016016
cette dernière ést= à 1 -2004/4016016 ,en réduisant au même dénominateuron obtient la forme a/b où a et b sont des nombres entiers naturels

Posté par
link224re : ENIGMA 16: Tue-Racines** 17-02-08 à 10:44

gagnéSalut!

Posons x=\frac{1}{(k\sqrt{k+1}+(k+1)\sqrt{k})}
On multiplie par l'expression conjuguée, et on obtient :
x=\frac{k\sqrt{k+1}-(k+1)\sqrt{k}}{k^2(k+1)-(k+1)^2k} soit, après simplification du dénominateur :

x=\frac{k\sqrt{k+1}-(k+1)\sqrt{k}}{-k(k+1)}
D'où, en séparant en 2,

x=\frac{-sqrt{k+1}}{k+1}+\frac{sqrt{k}}{k}

On a donc :

\sum_{k=1}^{4016015} x = -\frac{sqrt{2}}{2}+sqrt{1}-\frac{sqrt{3}}{3}+\frac{sqrt{2}}{2}-...-\frac{sqrt{4016016}}{4016016}+\frac{sqrt{4016015}}{4016015}

Ainsi, les termes s'éliminent 2 par 2, et il reste :

\sum_{k=1}^{4016015} x = sqrt{1}-\frac{sqrt{4016016}}{4016016} = 1-\frac{1}{sqrt{4016016}}

Or sqrt{4016016}=2004
Donc \sum_{k=1}^{4016015} x = 1-\frac{1}{2004} = \frac{2003}{2004}

Donc a=2003 et b=2004. J'espère que la démonstration est correcte.

@+ et merci pour l'énigme

Posté par
MataHitiennere : ENIGMA 16: Tue-Racines** 17-02-08 à 13:48

gagnéB'jour,

On a :
\frac{1}{k sqrt{k+1} + (k+1) sqrt{k}}

= \frac{(k+1) sqrt{k} - k sqrt{k+1}}{(k+1) sqrt{k} - k sqrt{k+1}} \times \frac{1}{(k+1) sqrt{k} + k sqrt{k+1}}

= \frac{(k+1) sqrt{k} - k sqrt{k+1}}{ k(k+1)^2 - k^2 (k+1)}

= \frac{(k+1) sqrt{k} - k sqrt{k+1}}{k (k+1)} \times \frac{1}{k+1-k}

= \frac{(k+1) sqrt{k} - k sqrt{k+1}}{k (k+1)}

= \frac{sqrt{k}}{k} - \frac{sqrt{k+1}}{k+1}

Par télescopage, on a donc :
\Bigsum_{k=1}^{4016015} \frac{1}{k sqrt{k+1} + (k+1) sqrt{k}} = \Bigsum_{k=1}^{4016015} \frac{sqrt{k}}{k} - \frac{sqrt{k+1}}{k+1} = 1 - \frac{sqrt{4016016}}{4016016} = 1- \frac{1}{sqrt{4016016}}

Or, 40.160.16 = 4*10^6 + 16.000 + 4^2 = (2*10^3)^2 + 4^2 + 2*2*10^3 *4 = (2*10^3+4)^2 = 2004^2

Donc : \Bigsum_{k=1}^{4016015} \frac{1}{k sqrt{k+1} + (k+1) sqrt{k}} = 1- \frac{1}{2004} = \frac{2003}{2004}

a=2003
b=2004

Posté par
LaboTue-Racines** 17-02-08 à 15:29

gagné1/(k(k+1)+(k+1)k)=1*(k(k+1)-(k+1)k)/(k(k+1)+(k+1)k)*(k(k+1)-(k+1)k)=
(k(k+1)-(k+1)/(k²(k+1)-(k+1)²k)=(k(k+1)-(k+1)/(-k(k+1))=-1/((k+1))+1/k
d'où=-1/2  +1/1 -1/3 +2  -1/4  +1/3-.............-1/401615 +1/401614 -1/401616+ 1/401615 =1 - 1/2004=2003/2004  
a=2003 et b=2004  

Posté par
piepalmre : ENIGMA 16: Tue-Racines** 17-02-08 à 17:35

gagnéSoit S la somme cherchée.
1/((k+1)rac(k)+k*rac(k+1))=((k+1)rac(k)-k*rac(k+1))/k(k+1)=1/rac(k)-1/rac(k+1)
Donc S=1-1/rac(N+1) avec N=4016015; or rac(4016016)=2004
Donc S=2003/2004 et a=2003, b=2004

Posté par
toriotue racines 17-02-08 à 21:00

perdu2023/2024

A+
Torio

tue racines

Posté par
spencer(2003/2004) 20-02-08 à 13:45

gagné1/[(k(k+1))+((k+1)k)]
=[(k(k+1))-((k+1)k)]/[-k^2-k]
=k/k - (k+1)/(k+1)
=1/k - 1/(k+1)
apres il suffit d'additionner les nombres k de 1 à 4016015
et il va rester 1 - 1/2004=(2003/2004)

Posté par
papagonre : ENIGMA 16: Tue-Racines** 20-02-08 à 19:28

gagnévoila ma réponse :

On a {{1}\over{\sqrt{k}\,\left(k+1\right)+k\,\sqrt{k+1}}}

En multipliant par l'expression conjugée, on obtient :

{{\sqrt{k}\,\left(k+1\right)-k\,\sqrt{k+1}}\over{k^2+k}}

Soit : {{\sqrt{k}\,\left(k+1\right)}\over{k^2+k}}-{{1}\over{\sqrt{k+1}}}

Soit : {{1}\over{\sqrt{k}}}-{{1}\over{\sqrt{k+1}}}

Donc : \sum_{k=1}^{n}{{{1}\over{\sqrt{k}\,\left(k+1\right)+k\,\sqrt{k+1}}} } = \sum_{k=1}^{n}{{{1}\over{\sqrt{k}}}-{{1}\over{\sqrt{k+1}}}}

Cette somme se simplifie en : 1-{{1}\over{\sqrt{n+1}}}

La racine carrée de 4016015+1 est 2004
Donc \sum_{k=1}^{4016015}{{{1}\over{\sqrt{k}\,\left(k+1\right)+k\,\sqrt{k+1}}} } = 1-1/2004 = 2003/2004
a = 2003 b = 2004 !

Posté par
Moumbore : ENIGMA 16: Tue-Racines** 21-02-08 à 18:10

perduBonjour une bonne énigme,
Posons Vn \bigsum_{k=1}^n \frac{1}{k\sqrt{kn}+(k+1)\sqrt{kn}} = \bigsum_{k=1}^n u_k \\ avec u_k=\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}

uk= \frac{(k\sqrt{k+1}-(k+1)\sqrt{k})}{(k\sqrt{k+1}+(k+1)\sqrt{k})(k\sqrt{k+1}-(k+1)\sqrt{k})=\frac{k\sqrt{k+1}-(k+1)\sqrt{k}}{k^2(k+1)-(k+1)^2k

uk=\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{(k+1)^2k-k^2(k+1)=\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{k^2+k}=\frac{(k+1)(\sqrt{k}-k\sqrt{k+1}}{k(k+1)

Vn= u1+\bigsum_{k=2}^{n-1} u_k+u_n = \frac{2\sqrt{1}-1\sqrt{2}}{1x2}+[\bigsum_{k=2}^{n-1}\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{k(k+1)}]+\frac{(n+1)\sqrt{n}-n\sqrt{n+1}}{n(n+1)

Posté par
Moumbore : ENIGMA 16: Tue-Racines** 21-02-08 à 18:11

perduDonc c'est 2007001/2007008

Posté par
gloubire : ENIGMA 16: Tue-Racines** 22-02-08 à 11:54

gagnéBonjour,

Etudions la suite U définie par U0 = 0 et Un = Un-1 + \rm%20\frac{1}{n\sqrt{n+1}+(n+1)\sqrt{n}}

En effet, \rm%20\Bigsum_{k=1}^{4016015}\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} = U4016015


Voyons les premiers termes:

U1 = \rm%200+\frac{1}{\sqrt{2}+2} = \frac{{2-\sqrt{2}}}{(2+\sqrt{2})(2-\sqrt{2})} = \frac{{2-\sqrt{2}}}{4-2} = 1-\frac{{\sqrt{2}}}{2}

U2 = \rm%201-\frac{{\sqrt{2}}}{2}+\frac{1}{2\sqrt{3}+3\sqrt{2}} = 1-\frac{{\sqrt{2}}}{2}+\frac{3\sqrt{2}-2\sqrt{3}}{(3\sqrt{2}+2\sqrt{3})(3\sqrt{2}-2\sqrt{3})} = 1-\frac{{\sqrt{2}}}{2}+\frac{3\sqrt{2}-2\sqrt{3}}{6} = 1-\frac{{\sqrt{3}}}{3}


On peut raisonnablement conjecturer que Un = 1-\frac{sqrt{n+1}}{n+1}

Une petite récurrence devrait suffire.

La formule est vraie pour n = 1.
Il reste à montrer que si elle est vraie pour n, elle l'est également pour n+1, autrement dit que

1-\frac{sqrt{n+2}}{n+2} = 1-\frac{sqrt{n+1}}{n+1} + \frac{1}{(n+1)\sqrt{n+2}+(n+2)\sqrt{n+1}}

Cette expression équivaut à:

\frac{sqrt{n+1}}{n+1}-\frac{sqrt{n+2}}{n+2} = \frac{1}{(n+1)\sqrt{n+2}+(n+2)\sqrt{n+1}}

\frac{(n+2)sqrt{n+1}-(n+1)sqrt{n+2}}{(n+1)(n+2)} = \frac{1}{(n+1)\sqrt{n+2}+(n+2)\sqrt{n+1}}

[(n+2)\sqrt{n+1}+(n+1)\sqrt{n+2}].[(n+2)\sqrt{n+1}-(n+1)\sqrt{n+2}] = (n+2)(n+1)

(n+2)2(n+1)-(n+1)2(n+2) = (n+2)(n+1)

(n+2)(n+1)(n+2-n-1) = (n+2)(n+1)

(n+2)(n+1) = (n+2)(n+1)  CQFD

Donc \rm%20\Bigsum_{k=1}^{4016015}\frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} = 1-\frac{sqrt{401615+1}}{401615+1} = \frac{2004.2004-2004}{2004.2004} = \frac{2004-1}{2004} = \frac{2003}{2004}

Ouf!
Soyez indulgents, c'est mon baptême du feu avec Latex...


A+,
gloubi

Posté par
dhaltere : ENIGMA 16: Tue-Racines** 27-02-08 à 10:05

gagnéBonjour
\frac1{k\sqr{k+1}+(k+1)\sqr{k}}=\frac1{\sqr{k}}-\frac1{\sqr{k+1}}
donc \displaystyle \sum_1^n \frac1{k\sqr{k+1}+(k+1)\sqr{k}} = 1-\frac1{\sqr{n+1}}
4012015+1=(2004)^2
donc \displaystyle \sum_1^{401615} \frac1{k\sqr{k+1}+(k+1)\sqr{k}} = 1-\frac1{2004}=\frac{2003}{2004}

Posté par
ThierryMasulaENIGMA 16: Tue-Racines 28-02-08 à 13:09

gagnéSimplifions :

\frac{1}{k sqrt (k+1) + sqrt k (k+1)}
= \frac{1}{sqrt k sqrt (k+1) (sqrt (k+1) + sqrt k)}
= \frac{1}{sqrt k sqrt (k+1) (sqrt (k+1) + sqrt k)}\frac{sqrt (k+1) - sqrt k}{sqrt (k+1) - sqrt k}
= \frac{sqrt (k+1) - sqrt k}{sqrt (k+1) sqrt k ((k+1)-k)}
= \frac{sqrt (k+1)-sqrt k}{sqrt (k+1) sqrt k}
= \frac{1}{sqrt k}-\frac{1}{sqrt (k+1)}

En remplaçant cette dernière expression dans la somme proposée,
on s'aperçoit que les termes s'annulent de proche en proche.

Donc :

\sum_{k=1}^{4016015} \frac{1}{k sqrt (k+1) + sqrt k (k+1)}
= \frac{1}{sqrt 1} - \frac{1}{sqrt (k+1)} où k=4016015

Remarquons que 4016015+1 est un carré parfait. Dingue!
sqrt {4016016}=2004

La solution est donc :

1-\frac{1}{2004}

ou encore

\frac{2003}{2004}

Posté par
EmAlPare : ENIGMA 16: Tue-Racines** 01-03-08 à 00:39

gagnéOn a : 1/(k(k+1)+(k+1)k)=(k(k+1)-(k+1)k)/(k²(k+1)-(k+1)²k)
=(k(k+1)-(k+1)k)/(k(k+1)(k-(k+1))
=k/k-(k+1)/(k+1)
=1/k-1/(k+1)

Donc S= (1/1)-(1/2)+(1/2)-(1/3)+.....-(1/4016016)=1-1/2004=2003/2004

Donc a=2003 et b=2004

Posté par
lo5707re : ENIGMA 16: Tue-Racines** 03-03-08 à 12:43

perduBonjour,

J'ai commencé par calculer \bigsum_{k=1}^N \frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} pour des petites valeurs de N.
J'ai trouvé que pour N=3, la somme vallait 1/2, pour N=8: 2/3.
Après, j'avoue m'être servi d'Excel pour trouver les valeurs suivantes...
N=15: 3/4
N=24: 4/5
N=35: 5/6
etc...

Les valeurs de N donnant une valeur rationnelle sont définis par la suite:
u1=3
un=un-1+2n+1

Ce qui donne:
un=n²+2n

L'expression \bigsum_{k=1}^{4016015} \frac{1}{k\sqrt{k+1}+(k+1)\sqrt{k}} sera rationnelle si 4016015 est de la forme n²+2n et vaudra \frac{n}{n+1}

Ici encore je me suis aidé d'Excel... pour trouver que 4016015 = 2003² + 2*2003

L'expression vaut donc: \frac{2003}{2004}

a=2003 et b=2004


Je sais qu'il est précisé que l'on ne peut pas utiliser de calculatrice ou de programme, mais je n'ai utilisé Excel que très peu et pour de petits calculs, la démarche de réflexion est quand même là.
Mais bon j'accepterai quand même le poisson...


Merci pour cette énigme.

Posté par
monrow Posteur d'énigmesre : ENIGMA 16: Tue-Racines** 04-03-08 à 20:24

ENIGME CLOTUREE

Désolé pour Torio qui a juste commis une très petite faute de calcul, et lo5707

lune et étoile aussi était dans ses derniers calculs ... mais déterminer la valeur de a et b était obligatoire (qui sait qu'on va faire une petite erreur de calcul comme ce qui est arrivé à torio ...)

Merci pour votre participation

Posté par
lo5707re : ENIGMA 16: Tue-Racines** 06-03-08 à 15:36

perduTant pis...

Challenge (énigme mathématique) terminé .
Nombre de participations : 0
:)0,00 %0,00 %:(
0 0

Temps de réponse moyen : 109:57:35.

Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !