Inscription / Connexion Nouveau Sujet
Enigmo 23 : Des cubes pour "Mini-Minkus" 

Bonjour,
Minkus a décidé de mettre "Mini-Minkus" aux énigmes de maths très tôt (voir ici : ![]() Finies les Minkuseries ? ).
Finies les Minkuseries ? ).
Voilà le jeu qu'il lui a proposé :
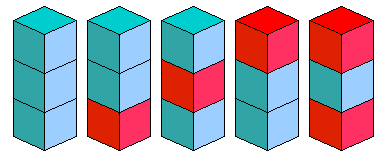
on dispose de cubes rouges et bleus, et le but est de les empiler pour réaliser une tour en respectant l'unique règle suivante : il ne doit pas y avoir deux étages rouges consécutifs.
L'image ci-dessous montre qu'on peut réaliser 5 tours différentes de 3 étages.
Question : combien de tours différentes de 12 étages peut-on réaliser ?
Question subsidiaire (ne compte pas pour l'énigme) : combien de tours à n étages ?
 Bonjour,
Bonjour,
Combien de tours à étages ?
Soit le nombre cherché.
Pour construire une telle tour, on peut prendre entre 0 et (partie entière) cubes rouges.
Soit le nombre de tours à
cubes dont
rouges :
Pour calculer , il suffit de s'apercevoir qu'on peut mettre (ou pas) un cube rouge tout en bas ou au-dessus de chacun des
cubes bleus :
Finalement :
(*)
On calcule :
T(3) = 5
T(4) = 8
T(5) = 13
...
On reconnaît la suite des nombres de Fibonacci, et on conjecture que :
où est défini par
,
,
Sauf erreur.
Merci pour l'énigme,
Nicolas
 On arrive facilement par récurrence à la suite de la forme u n+1=un+u n-1, avec u0=1 et u1=2.
On arrive facilement par récurrence à la suite de la forme u n+1=un+u n-1, avec u0=1 et u1=2.
En effet, pour obtenir un groupe de cubes à partir d'un groupe existant, on peut :
- rajouter au groupe des cubes bleus (un)
- rajouter au groupe ayant un cube bleu au sommet des cubes rouges (un-1)
On reconnaît la fameuse suite de Fibonacci.
Il y a 377 tours différentes de 12 étages.
La solution générique est (pour n étages ):
f (n) = (((1+sqrt(5))/2)^(n+2)-((1-sqrt(5))/2)^(n+2))/sqrt(5).
 Bonjour Jamo!
Bonjour Jamo! 
Voilà je fais confiance à mon programme, qui me dit :
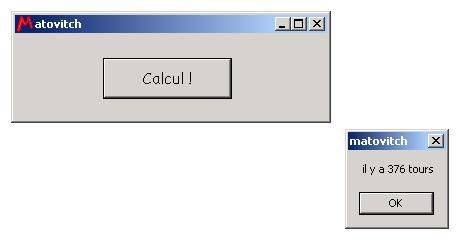
Je trouve qu'il y a donc 376 tours! 
 Arg!!! J'ai oublié une combinaison dans mon programme!
Arg!!! J'ai oublié une combinaison dans mon programme!
Il y a 377 tours !
Voici la suite que je trouve grâce à mon programme :
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...
Il s'agit de la suite de Fibonacci (sans le 1 au départ) ! 
Je suis vraiment dégouté !
 bonjour Jamo et Minkus et bienvenue à Dilia-Aurora !
bonjour Jamo et Minkus et bienvenue à Dilia-Aurora !
il y a trois cent septante-sept façons d'empiler les cubes selon la règle
la formule générale pour n cubes = (n+2)ième nombre de Fibonacci
soit E(n) le nombre d'empilements de n cubes
supposons qu'on soit en présence de tous les empilements possibles de n cubes
pour créer des empilements de (n+1) cubes
on peut mettre un cube bleu au-dessus de chacun : E(n)
on peut mettre un cube rouge au-dessus, à condition que le cube supérieur soit bleu; les empilements au cube supérieur bleu proviennent des empilements de (n-1) cubes auxquels on a ajouté un cube bleu; ils sont au nombre de E(n-1)
au total E(n+1) = E(n)+E(n-1)
 Salut jamo
Salut jamo 
Une enigme similaire a ete proposee recemment... en tout cas voici la solution:
n cubes
01 2
02 3
03 5
04 8
05 13
06 21
07 34
08 55
09 89
10 144
11 233
12 377
La suite de Fibonacci: F0=0 ; F1=1 ; F2=1 ; F3=2 ; F4=3 ; ...
Alors pour n etages, le nombre de possibilites sera F(n-2)

 Bonsoir,
Bonsoir,
Fibonacci quand tu nous tiens...
Sans produire le détail par type, on obtient pour n=12, 377 piles possibles parmi les
Le cas général se calcule via la formule de Binet (avec décalage de deux rangs):
.
Merci pour cette énigme sympa.
 Hello,
Hello,
je me suis servie des nombres en base 2 avec 0 = cube bleu et 1 = cube rouge
voici un exemple de séries qui conviennent :
000000000000
000000000001
000000000010
000000000100
000000000101
000000001000
000000001001
000000001010
000000010000
000000010001
000000010010
000000010100
000000010101
000000100000
000000100001
ma réponse : 377 tours différentes de 12 étages 

Question subsidiaire (ne compte pas pour l'énigme) : combien de tours à n étages ?
On demande à Fibonacci ?

 Bonjour
Bonjour
cela ressemble beaucoup à Fibonacci...
pour n = 12, il y a 377 étages possibles
pour tout n, il y a ( φ^(n+2) - (1-φ)^(n+2) ) / √5
ou φ est le nombre d'or ( 1+√5 )/2
Merci
Mathieu
 Bonjour Jamo
Bonjour Jamo
J'ajoute le nombre de tours surmontées d'un cube bleu à celles surmontées d'un cube rouge.
Ainsi, l'exemple fourni par l'énoncé me donne
n3= 3 + 2 donc
n4= 5 + 3 donc
n5= 8 + 5 donc
n6= 13 + 8
n7= 21 + 13
n8= 34 + 21
n9= 55 + 34
n10= 89 + 55
n11=144 + 89
n12=233 + 144
ce qui donne donc 377 tours de 12 étages
 Bonjour Jamo et toutes mes félicitations à Minkus,
Bonjour Jamo et toutes mes félicitations à Minkus,
Pour résoudre le problème, on procède par itérations à partir (et au-delà) de 3 étages.
Pour une tour de n étages où le rez est bleu, les étages au dessus de celui-ci forment une tour de n-1 étages devant répondre aux conditions de l'énoncé.
Si le rez est rouge, le premier étage doit être bleu et les étages au dessus du premier forment une tour de n-2 étages devant répondre aux conditions de l'énoncé.
On tombe bien évidemment sur la suite de Fibonacci et la solution pour une tour de n étages est .
Dans le cas particulier des tours à 12 étages la solution est donc 377 tours différentes.
 Bonjour,
Bonjour,
En lisant l'énigme j'ai pensé au problème du sac à dos. Je m'y suis inspirée pour faire une récurrence sur n le nombre d'étages et je pose P(n) le nombre de tours admissibles d'hauteur n.
P(1)=2
Si je parcours la tour de bas en haut, je nomme l'étage du premier cube rouge. Pour k fixé, le nombre de tours possibles est le nombre de tours de hauteur n-k-1 (ce qu'il y a au dessus de l'étage k+1, qui est bleu). Donc
avec la convention que P(0)=P(-1)=1. (C'est pour les cas où k=n-1 ou k=n, où on n'a qu'une possibilité à comptabiliser car on ne peut pas mettre d'autres cubes rouges dans la tour.) Un petit changement de variable et j'ai
.
Je calcule les premiers termes et je me rends compte que ma formule est en fait une propriété de la suite de Fibonacci, avec un petit décalage dans les termes: P(n)=F(n+2).
Le nombre de tours de 12 étages est donc P(12)=F(14)=377.
Pour les tours à n étages, je me contente de dire qu'il y en a F(n+2), ce n'est pas la peine que je sorte la formule de Binet ou autres méthodes de calcul, on les trouve partout sur le net.
 Isis
Isis
 Bonjour,
Bonjour,
On a ici à faire à la suite de Fibonacci.
1 cube: 2 tours
2 cubes: 3 tours
3 cubes: 5 tours
4 cubes: 8 tours
...
12 cubes: 377 tours
...
n cubes: "le (n+2)ème nombre de Fibonacci" tours.
J'avais déjà donné 2 JFF comme celle-là: ![]() JFF_Les cubes du père Spective ,
JFF_Les cubes du père Spective , ![]() JFF_suites de x et de y
JFF_suites de x et de y
Merci pour cette énigme.
 Dans une des t(n) tours de n étages, l'étage inférieur est soit bleu, soit rouge.
Dans une des t(n) tours de n étages, l'étage inférieur est soit bleu, soit rouge.
S'il est bleu, les étages au dessus forment une des t(n-1) tours de n-1 étage possible.
S'il est rouge, le second étage est obligatoirement bleu, et les étages au dessus forment une des t(n-2) tours de n-2 étages possibles. On a donc t(n)=t(n-1)=t(n-2), avec t(0)=1, t(1)=2, t(2)=3,...on reconnait la suite de Fibonacci (avec les notations classiques t(n)=F(n+2): t(3)=5, t(4)=8, t(5)=13, t(6)=21, t(7)=34, t(8)=55, t(9)=89, t(10)=144, t(11)=233, t(12)=377 qui est le nombre cherché.
 Bonjour
Bonjour
Ah Fibonacci, quand tu nous tiens...
Classons donc les tours en deux catégories, celles qui se terminent par un cube rouge et celles qui se terminent par un cube vert, (non, bleu, je blague)
Soit le nombre de tours à n étages se terminant par un cube rouge
Soit le nombre de tours à n étages se terminant par un cube bleu
Evidemment, on cherche
Combien de tours à n+1 étages va-t-on pouvoir construire à partir de ces tours à n étages ?
On prend celles se terminant par un cube rouge : on ne peut que leur ajouter un cube bleu
On prend celles se terminant par un cube bleu : on peut leur ajouter un cube bleu ou un cube rouge
Donc nous pouvons calculer et
On peut calculer
Il nous faut résoudre cette équation
avec les conditions aux limites
et comme je suis feignant, je calcule aussi , même si physiquement, ça n'a aucun sens, cette valeur nous simplifie le calcul de la solution :
a pour solution générale une équation de la forme
(je vous passe le détail des considérations théoriques)
où sont solutions de l'équation
On trouve et
et pour trouver A et B, on soumet l'équation aux conditions initiales.
On trouve finalement
et
Il reste à calculer
Evidemment, cette formule donne le nombre de tours dans le cas général, puis on peut l'utiliser pour calculer le nombre de tours de 12 étages
Ce qui nous donne
Mais on pouvait se contenter, pour calculer le résultat attendu, de dresser le tableau des valeurs successives de à partir des relations de récurrence
Bonne soirée
 Je dirais 288 possibilités...
Je dirais 288 possibilités...
J'avoue, un petit programme informatique m'a aidé!!! (En esperant que je ne sois pas trompé en programmant...).
 Allez je me lance
Allez je me lance  ,
,
Selon moi, on peut réaliser 1036 tours différentes de 12 étages en respectant la règle : "il ne doit pas y avoir deux étages rouges consécutifs."
J'ai obtenu ce résultat par une série de calculs (et un peu par hasard il faut le dire  ) qui m'amène à une formule étrange :
) qui m'amène à une formule étrange : où
est un multiple de 2 (dans le cas de 12 étages
).
Bon, en espérant un  (mais j'ai des gros doutes sur cette énigme).
(mais j'ai des gros doutes sur cette énigme).
@+
 Bonjour,
Bonjour,
Pour 1 étage, on a 2 tours possibles
2 étages, 3 tours
3 étages, 5 tours
4 étages, 8 tours
etc.
On reconnait les termes successifs de la suite de Fibonacci.
Pour 12 étages, on a 377 tours réalisables.
A+, 
 Bonjour Jamo,
Bonjour Jamo,
nombre de tours possibles pour n=12
1+12+(10*11/2!)+(8*9*10/3!)+(6*7*8*9/4!)+(4*5*6*7*8/5!)+2=1+12+56+120+126+56+2=373
pour n=2k
nombre de tours avec aucun cube rouge=1
nombre de tours avec 1 cube rouge =n
nombre de tours avec 2 cubes rouges=(n-2)(n-1)/2!
nombre de tours avec 3 cubes rouges=(n-4)(n-3)(n-2)/3!.....
nombre de tours avec (k-1) cubes rouges=(n-2(k-1)+2))*(n-2(k-1)+3)...*(n-2(k-1)+k)/(k-1)!
nombre de tours avec k cubes rouges =2
pour n=2k-1
idem sauf pour k cubes rouges =1 possibilité
 Bonjour,
Bonjour,
Après avoir dénombré jusqu'à 8 étages :
T(0) = 0
T(1) = 2
T(2) = 3
T(3) = 5
T(4) = 8
T(5) = 13
T(6) = 21
T(7) = 34
T(8) = 55
...
Ça ressemble à la suite de Fibo (sauf le début qui est 1, 1, 2 ...) avec un décalage
Je pense qu'on peut réaliser différentes de 12 étages.
Je cherche pour n étages....
Merci Jamo. A+, KiKo21.
 Re-bonjour,
Re-bonjour,
Question subsidiaire (ne compte pas pour l'énigme) : combien de tours à n étages ?
A+, KiKo21.
 Bonjour,
Bonjour,
On peut réaliser 372 tours différentes de 12 étages.
Voici le détail:
12 cubes bleus : 1 tour.
11 cubes bleus 1 cube rouge : 12 tours.
10 cubes bleus 2 cubes rouges : 55 tours.
9 cubes bleus 3 cubes rouges : 120 tours.
8 cubes bleus 4 cubes rouges : 126 tours.
7 cubes bleus 5 cubes rouges : 51 tours.
6 cubes bleus 6 cubes rouges : 7 tours.
 Soit rn le nombre de tours de n étages se terminant par un cube rouge
Soit rn le nombre de tours de n étages se terminant par un cube rouge
et bn le nombre de tours de n étages se terminant par un cube bleu
Le nombre total de tours de n étages sera alors tn=rn+bn
Une tour de 1 étage peut être bleue ou rouge donc r1=1 et b1=1
Si le dernier étage d'une tour de n étages est rouge on est assuré que l'avant dernier est bleu donc rn=bn-1
Si le dernier étage est bleu l'avant dernier peut être bleu ou rouge donc bn=bn-1+rn-1
On a alors tn=bn+rn=bn-1+rn-1+bn-1=bn-1+rn-1+bn-2+rn-2=tn-1+tn-2 (suite de finonacci)
Finalement t12=377
On pourra donc construire 377 tours de 12 étages en respectant la règle
 c'est une progression suivant la suite de fibonacci:
c'est une progression suivant la suite de fibonacci:
à 12 étages, on peut ainsi former 377 tours différentes.
sauf erreur.
 Bonjour !
Bonjour !
Voici ma réponse : 1) pour 12 cubes, 144 possibilités
Question subsidiaire : Nn = 1/ 5 ((
5 (( )^n + (1-
)^n + (1- )^n), avec
)^n), avec  =(1+
=(1+ 5)/2
5)/2
Remarque : lien direct avec la suite de Fibonacci
puisque N(n+2) = B(n+2) + R(n+2) = N(n+1) + B(n+1) = N(n+1) + N(n)
Un coup d'intuition, j'espère que c'st juste. En tout cas merci pour l'énigme !
 Avec aucun cube rouge, on peut faire 1 tour
Avec aucun cube rouge, on peut faire 1 tour
Avec un cube rouge, on peut faire 12 tours
Avec deux cubes rouges, on peut faire 55 tours (1+2+3+4+5+6+7+8+9+10)
Avec trois cubes rouges, on peut faire 330 tours.(1+4+10+20+35+56+84+120)
Avec 4 cubes rouges, on peut faire 126 tours.(1+4+10+20+35+56)
Avec 5 cubes rouges, on peut faire 35 tours.(1+4+10+20)
Avec 6 cubes rouges, on peut faire 5 tours.(1+4)
Et c'est tout... mais c'est déjà pas mal !
Ca nous fait donc 564 tours.
Clôture de l'énigme
Bravo à tous ceux quoi ont trouvé. En effet, c'était encore un coup à Fibonacci pour ce problème !
matovitch >> en effet, ton programme a oublié une solution ... à moins que tu n'aies oublié de dire à ton programme de te la donner, non ? 
Angus >> je crois que tu as un petit décalage dans ta formule : pour une tour de n étages, c'est le (n+2)ème nombre de Fibonacci, pas le nème ...
Einsthein >> c'est la 1ère réponse qui compte ... mais même ta 2ème réponse n'est pas bonne.
D'autres semblent avoir utilisé des méthodes de dénombrement que je n'ai pas cherché à comprendre ...
 Juste une question, est ce que m'a gnééralisation est bonne, j'ai quelque doute, je n'ai aps la me^mee que les autres, mais c'est peut-être équivalent
Juste une question, est ce que m'a gnééralisation est bonne, j'ai quelque doute, je n'ai aps la me^mee que les autres, mais c'est peut-être équivalent 

D'autres semblent avoir utilisé des méthodes de dénombrement que je n'ai pas cherché à comprendre ...
Les nombres en base 2 ?

Bravo à tous les récipiendaires 
Etonnants, ces posts, non ?


--------------------------
J'ai bien aimé aussi celui-là :
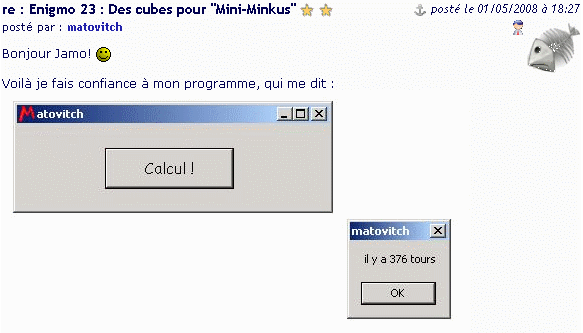
Sans rancume matovitch


salut kiko21 
mais matovitch est un JFFien également : il ne fait pas que les z'officielles, il s'amuse aussi avec les JFF...
et on se connaît bien maintenant, je sais qu'il ne le prendra pas mal, à sa juste valeur de joke 
je t'avouerai que je ne ferais pas ce type de remarque à d'autres mathîlien(ne)s, à l'humour plus...délicat 

Nombre de participations : 0
Temps de réponse moyen : 93:01:03.



