Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première DérivationTopics traitant de dérivation [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

fonctions

Posté par
lugia 15-08-07 à 23:36

Bonjour, voilà j'ai un exercice sur les fonctions et j'aimerai savoir si ce que j'ai fais est pour l'instant bon ou non et si vous pourriez m'aider a rectifier mes erreurs svp. Voilà l'énoncé, merci :
On considère la fonction f(x) définie sur I = ]-oo;2[union]2;+oo[ par f(x) = (x/4)+(1/x-2) et on note C la courbe représentative de f dans un repère orthogonal (O ; i ; j ) avec pour unités graphiques : 1 cm sur l'axe des abscisses et 2 cm sur l'axe des ordonnées.
1) Déterminer le sens de variation de f.
2) Déterminer les limites de f aux bornes de I
3)  Montrer que C admet deux asymptotes
4)  Etablir le tableau de variations de f.
5)  Déterminer la position de C et de son asymptote oblique
6)  Tracer les asymptotes à C, les tangentes horizontales éventuelles à C puis C
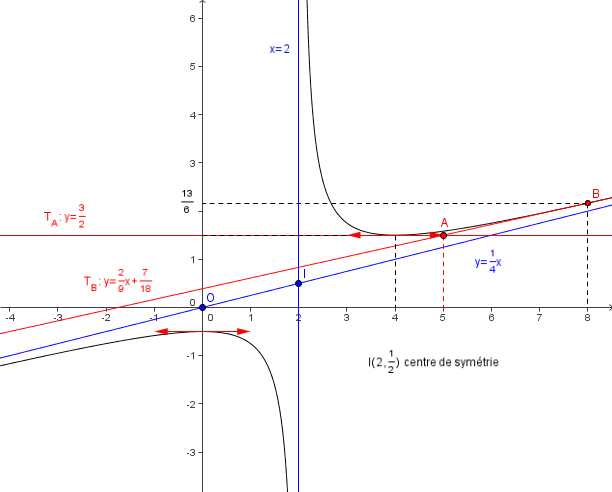
7) a)Déterminer une équation de TA la tangente à C au point A d'abscisse 4 puis de TB la tangente à C au point B d'abscisse 8 .
b)Tracer TA et TB. Calculer les coordonnées du point d'intersection de ces deux tangentes.
8)  Démontrer que : pour tout réel x de [3 ; 5], 3/2inférieur ou égal f(x)inférieur ou égal 7/4.

9) Montrer que C admet un centre de symétrie.

Voilà ce que j'ai fait. J'aimerai savoir si c'est bon ou pas pour l'instant. Merci
1) Soit f(x) = (x/4)+(1/x-2) une fonction rationnelle donc dérivable en tout réel de son ensemble de définition I = ]-oo;2[union]2;+oo[
Pour ts x différent de 2
F'(x)= ((-1/((x-2)carré))+1/4)
Je vous épargne les calcules
(x-2)carré supérieur a 0 dc f'(x) inférieur a 0
F est donc décroissante sur]-oo;2[et]2;+oo[

2) on a f(x) = (x/4)+(1/x-2)
Lim x qd x tend vers + l'infini =+l infini dc Lim de x/4 qd x tend vers +l'infini=+l'infini car ¼ strictement sup a 0
Lim (1/x-2) qd x tend vers+l'infini=0
Lim x qd x tend vers -l'infini=- l'infini dc Lim x/4 qd x tend vers -l'infini= -l'infini car ¼ strictement sup a 0
Lim (1/x-2) qd x tend vers -l'infini=0
Lim de x qd x tend vers 2 par valeur inférieur a 2=-l'infini dc Lim de x/4 qd x tend vers 2 par valeur inférieur a 2=-l'infini
Lim de x qd x tend vers 2 par valeur supérieur a 2=+l'infini dc Lim de x/4 qd x tend vers 2 par valeur supérieur a 2=+l'infini
Lim de (1/x-2) qd x tend vers 2 par valeur inférieur a 2=-l'infini
Lim de (1/x-2) qd x tend vers 2 par valeur supérieur a 2=+l'infini

Par addition
Lim f(x)qd x tend vers + l'infini =+l infini
Lim f(x)qd x tend vrs -l'infini=- l'infini
Lim de f(x) qd x tend vers 2 par valeur inférieur a 2=- l'infini
Lim de f(x) qd x tend vers 2 par valeur supérieur a 2=+l'infini
Pr les deux dernières lignes je ne suis pas très sur.

Ensuite pr démontrer que f a 2 asymptote, j'ai trouvé la première méthode av la première qui est y=1/4x la je suis sur dc je ne fais pas la démo. Mais pour l'autre asymptote je n'y arrive pas.
Jai établi le tableau de variation pr lequel je suis sur.
Puis pour la position de c et de son asymptote je fais la différence de f(x)-(1/4x)
J'étudie le signe de la différence et tous… là aussi ca va.
Ensuite ca se gatte j'aimerai savoir comment on fait pour répondre aux questions 8 et 9 svp.
Est-ce que vous pourriez me dire si ce que j'ai fais pour l'instant est correct ou non et me donner quelques indications svp.
Merci d'avance pour tout.

Posté par
gui_toure : fonctions 15-08-07 à 23:39

Bonsoir

Dis-moi, ta fonction c'est bien 4$ f(x)=\frac{x}{4}+\frac{1}{x-2} ? Non ?

Posté par
lugiare : fonctions 15-08-07 à 23:42

bonsoir
oui c'est bien ca

Posté par drioui (invité)re : fonctions 15-08-07 à 23:45

salut
essaye de determiner le signe de f'(x) pour cela tu dois reduire au meme denominateur

Posté par
gui_toure : fonctions 15-08-07 à 23:46

Je pense que tu as déduis un peu vite :

Citation :
(x-2)carré supérieur a 0 dc f'(x) inférieur a 0
F est donc décroissante sur]-oo;2[et]2;+oo[


d'accord pour (x-2)^2\ge0
mais ca ne dis en rien que f' est positive sur I !

Mets \frac{1}{4}-\frac{1}{(x-2)^2} sous le même dénominateur et dis moi si f' est positive sur I

Posté par
gui_toure : fonctions 15-08-07 à 23:48

Salut drioui

Posté par drioui (invité)re : fonctions 15-08-07 à 23:50

pour les limites c'est bon

Posté par drioui (invité)re : fonctions 15-08-07 à 23:51

salut  gui_tou

Posté par
gui_toure : fonctions 15-08-07 à 23:53

En ce qui concerne les asymptotes tu dois t'être embrouillé(e).

Ne pas confondre asymptote oblique et verticale.

Ici il n'y en a qu'une de chaque sorte.

Posté par
gui_toure : fonctions 15-08-07 à 23:55

Citation :
la première [asymptote]qui est y=1/4x




Elle est asymptote à C ? Sur quel intervalle ?

Posté par
lugiare : fonctions 16-08-07 à 00:35

Et bien je dis que la droite delta d'équation y=1/4x  est asymptote aC en + et - l'infini. Sinn je ne comprend pas ou est le problème
Merci pour le reste

Posté par
lugiare : fonctions 16-08-07 à 00:42

et quand je met au mème dénominateur et que je simplifie je trouve f(x) négatif

Posté par
lugiare : fonctions 16-08-07 à 00:43

enfin nn
jai fais une erreur

Posté par
lugiare : fonctions 16-08-07 à 00:50

non c'est bien ça f' est négatif sur I je crois

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 10:45

Bonjour,

Tes limites sont justes.
L' asymptote oblique d' équation 3$y=\frac{1}{4}x aussi.

Pour la seconde asymptote:
Tu as des limites infinies en 2 (valeur interdite): cela signifie que la droite verticale d' équation 3$x=2 est asymptote à (C).

Pour les variations, ça se gâte:

Tu as: 3$f'(x)=\frac{1}{4}-\frac{1}{(x-2)^2}=\frac{x(x-4)}{4(x-2)^2}

A toi d' étudier le signe de cette dérivée pour avoir les variations...

On ne peut guère faire la 8 et la 9 avant d' avoir les variations de ta fonction et tracé la courbe.

Posté par
gui_toure : fonctions 16-08-07 à 11:12

Bonjour cailloux

Pour l'asymptote oblique j'avais lu 3$y=\frac{1}{4x}.

Attention à l'écriture  !

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 11:18

Bonjour gui_tou,

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 11:43

Re,

En principe tu dois obtenir un tableau de variation dans ce goût là:


4$\begin{tabular}{c|ccccccccc}x&-\infty& &0& &2& &&4& &+\infty\\\hline{f'(x)}&&+&0&-&||&&-&0&+&\\\hline\\{}&&&-\frac{1}{2}&&||&+\infty&&&&+\infty\\{f(x)}&&\nearrow&&\searrow&||&&\searrow&&\nearrow\\{}&-\infty&&&-\infty&||&&&\frac{3}{2}\\\end{tabular}


Une accolade dont je n' arrive pas à me débarasser

Posté par
gui_toure : fonctions 16-08-07 à 11:45

Très joli

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 11:49

Mon premier Quelle galère!

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 12:26

...et cette courbe:
fonctions

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 13:28

8) Sur 3$[3,4], 3$f est décroissante d' où 3$f(4)\leq f(x)\leq f(3), c' est à dire 3$\frac{3}{2}\leq f(x)\leq \frac{7}{4}

Sur 3$[4,5], 3$f(x) est croissante d' où 3$f(4)\leq f(x)\leq f(5), c' est à dire 3$\frac{3}{2}\leq f(x)\leq \frac{19}{12}< \frac{7}{4}.

On en déduit que sur 3$[3,5], \frac{3}{2}\leq f(x)\leq \frac{7}{4}

9)Avec le graphe de la fonction 3$f, on peut conjecturer que le point 3$I(2,\frac{1}{2}), point d' intersections des asymptotes est centre de symétrie de la courbe.

Pour le démontrer, on peut utiliser plusieurs méthodes:

Changement d' origine du repère:

On fait une translation d' axes qui ramène l' origine du repère en I;

Soit 3$M un point de la courbe. Ses coordonnées sont 3$M(x,y) dans le repère 3$(O,\vec{i},\vec{j}) et M(X,Y) dans le repère 3$(I,\vec{i},\vec{j})

On a: 3$\vec{OM}=\vec{OI}+\vec{IM}

d' où l' on tire les formules de transformation:

3$\{x=2+X\\y=\frac{1}{2}+Y

Ici, le domaine de définition de 3$f est centré sur 2 et la première condition est réalisée.

On forme: 3$\frac{f(2+h)+f(2-h)}{2}=\frac{\frac{2+h}{4}+\frac{1}{h}+\frac{2-h}{4}-\frac{1}{h}}{2}=\frac{1}{2} l' équation 3$y=\frac{x}{4}+\frac{1}{x-2} dans le premier repère devient dans le second:

3$Y+\frac{1}{2}=\frac{X+2}{4}+\frac{1}{X}

soit; 3$Y=\frac{X}{4}+\frac{1}{X}=F(X) dans le nouveau repère d' origine 3$I
On remarque que: F(-X)=\frac{-X}{4}+\frac{1}{-X}=-(\frac{X}{4}+\frac{1}{X})=-F(X)

La foction 3$F est donc impaire et la courbe admet 3$I comme centre de symétrie dans le nouveau repère.

2ème méthode:
3$I(a,b)\,\, \text{centre\, de\, symetrie}\,\, \Longleftrightarrow \{a+x\in D_f \Rightarrow a-x \in D_f\\\forall h \,\,\text{tel\,que}\,\, a+h\in D_f,\,\,\frac{f(a+h)+f(a-h)}{2}=b

Ici, le domaine de définition de 3$f est centré sur la valeur 2 et la première condition est réalisée.

On forme: 3$\frac{f(2+h)+f(2-h)}{2}=\frac{\frac{2+h}{4}+\frac{1}{h}+\frac{2-h}{4}-\frac{1}{h}}{2}=\frac{1}{2}

Le point 3$I(2,\frac{1}{2}) est donc bien centre de symétrie de la courbe représentative de 3$f

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 13:33

Tiens, il y a eu un copier-coller malheureux...

Posté par
infophilere : fonctions 16-08-07 à 13:48

Joli

Pour faire encore plus beau tu peux fermer ton tableau

Posté par
lugiare : fonctions 16-08-07 à 13:51

merci beaucoup j'ai eu beaucoup plus que ce que j'attendais et merci pour tout le mal que vous vous etes donner. j'espère que maintenant quand je ferai d'autres exercice u type je comprendrai aussi bien. merci beaucoup bonne journée.

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 13:52

>> Kévin

Pour le tableau, j' ai déjà sué sang et eau!

Posté par
infophilere : fonctions 16-08-07 à 14:01

J'imagine ! Mon premier tableau était une catastrophe

Posté par
infophilere : fonctions 16-08-07 à 14:02

Je te laisse juger Problème Latex

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 14:05

Posté par
1 Schumi 1re : fonctions 16-08-07 à 14:46



Tu connaissais pas la fonction "prévisualisation"?

Posté par
Epicurienre : fonctions 16-08-07 à 16:52

Salut

Cailloux>>Comment fait  tu pour repérer un point comme cela avec geogebra?


Trés jolis posts


Kuider.

Posté par
cailloux Correcteurre : fonctions 16-08-07 à 17:04

>> Epicurien

Quand j' ai une fonction définie par 3$y=f(x), je saisis le point d' abscisse 3$a en faisant par exemple 3$A=(a,f(a)) dans la ligne de commande.

Je ne sais pas si cela répond à ta question...

Merci!

Posté par
Epicurienre : fonctions 16-08-07 à 17:08

Merci de la réponse!

Cela répond exactement à ma question

Kuider.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !