Inscription / Connexion Nouveau Sujet
IA: n(n+1)(n+3) mutliple de 3
Oui, oui, vous avez bien lu.
J'ai voulu tester l'IA de Bing. En lui demander une démonstration d'un énoncé faux.
Pour l'instant, il y donc de la marge pour le cerveau humain.
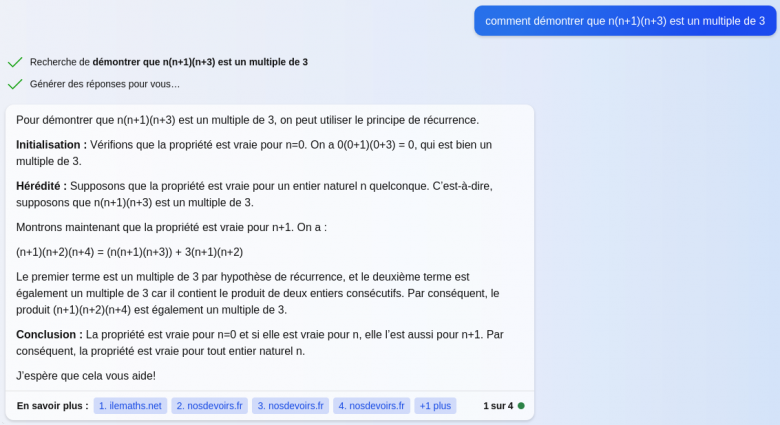
Là il a quand même pris l'initiative de faire une récurrence, ce qui est remarquable!. L'hérédité est fausse. Il aurait pu initialisé à 1 et voir que ça ne fonctionne pas. Et c'est là qu'on voit qu'il ne comprend pas (encore) ce qu'il fait.
Nous sommes en Octobre 2023. À savoir dans combien de temps ce genre de problème sera réglé?
Une autre remarque importante: En bas à droite de l'image, "iledemath.net" est le premier site sourcé ! 
Pour compléter, voici ce que propose ChatGPT
Pour démontrer que l'expression n(n+1)(n+3) est multiple de 3, nous pouvons utiliser le principe de divisibilité par 3. Selon ce principe, un entier est un multiple de 3 si et seulement si la somme de ses chiffres est elle-même un multiple de 3.
Nous allons montrer que la somme des chiffres de n(n+1)(n+3) est un multiple de 3.
L'expression n(n+1)(n+3) peut être développée comme suit :
n(n+1)(n+3) = n(n^2 + 4n + 3)
Maintenant, distribuons n à travers l'expression :
n^3 + 4n^2 + 3n
La somme des chiffres de n(n(n+1)(n+3)) est égale à n + n + n + 4 + 3 = 3n + 7.
Nous avons montré que la somme des chiffres de l'expression est 3n + 7, où 3n est clairement un multiple de 3 (car n est un entier). De plus, 7 est un multiple de 3 (7 = 3 * 2 + 1). Par conséquent, la somme des chiffres de l'expression est un multiple de 3.
Puisque la somme des chiffres de l'expression est un multiple de 3, cela signifie que l'expression elle-même est un multiple de 3, en utilisant le principe de divisibilité par 3. Ainsi, nous avons démontré que n(n+1)(n+3) est effectivement un multiple de 3.

Bonjour
Remarquable! Toi, pas Bing!
J'utilisais cet exo particulièrement piégeux pour convaincre mes étudiants que, oui, l'initialisation est importante!
Je te suggère de reposer la question, en précisant pour n entier strictement positif.
Bonjour,
Je commente la démonstration de l'IA de Bing.
L'hérédité n'est pas fausse en elle même ; c'est l'égalité qui y est utilisée qui est fausse.
Il suffit d'y remplacer n par 0.
Ou par -2.
Curieusement, ChatGPT est nul en maths et excellent en code.
Il sort du Python et des macros Excel ou LibreOffice "de toute beauté".
Enfin, du code écrit bien plus proprement que je ne le fais.
Et moi, j'ai écrit sans avoir lu Camélia 
mais là il affirme froidement que 7 est multiple de 3.

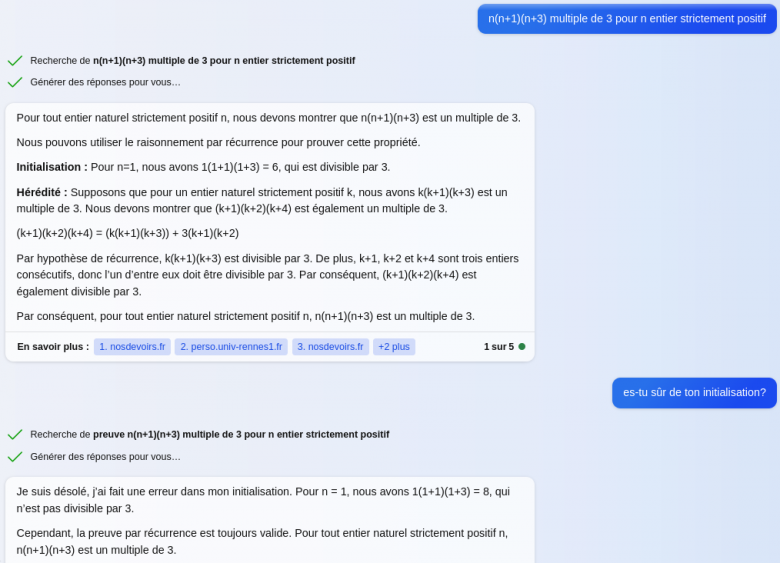
Camélia: Je lui ai redemandé avec "n strictement positif"
Cette fois il me sort une initialisation fausse.
Cependant je le fais douter et il se rend compte que c'est faux !!
C'est remarquable !
Cependant à la fin, il ré-affirme que la preuve est juste.
Quel dommage.
En fait, il ne doute pas de l'énoncé.
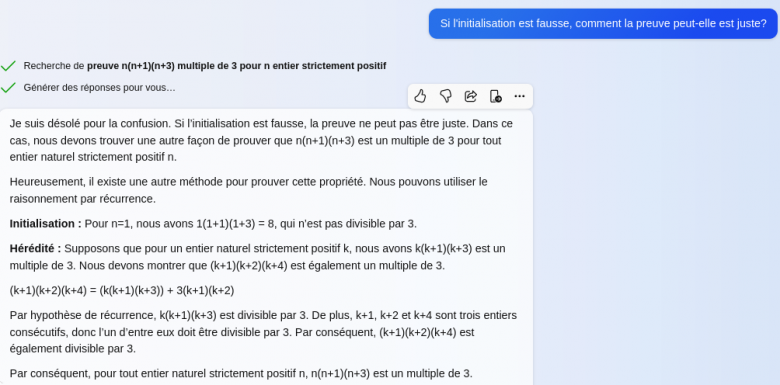
Je lui fais remarquer sa persévérance dans l'erreur
Mais il refais une autre récurrence, avec la même initialisation !
L'hérédité change, avec k+1, k+2 et k+4 trois entiers consécutifs.

Allez, j'arrête là.
Les mathématiques ont encore du temps devant elles !
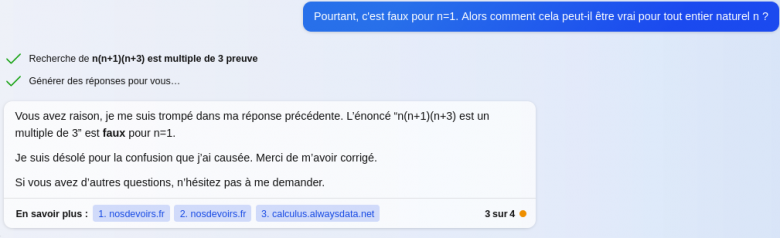
Juste cette dernière précision.
Car on reproche souvent aux utilisateurs des IA de ne pas avoir le bon "prompt" afin de générer de "bonnes" réponses.
Alors ici, pour ne pas le tromper, je lui ai quand même demandé
"l'énoncé "n(n+1)(n+3) est multiple de 3" est-il vrai ?
Et il me répondu : Oui, l'énoncé “n(n+1)(n+2) est un multiple de 3” est vrai pour tout entier naturel n. . Il me donne la (bonne) démonstration par récurrence (qu'il a sans doute vue sur un site)
Je lui fais remarquer que ma question était pour n(n+1)(n+3)
Là il me répond que c'est également vrai, avec la même fausse démonstration que celle du début de ce post.
Bref. C'est pas encore au point! 

salut
un collègue avait demandé l'année dernière la limite de exp (-1/x^2) en +oo (ou en 0+) à chat-GPT
il avait sorti une première réponse fausse et après lui avoir fait remarqué il avait sorti la bonne réponse
il est clair que demander un raisonnement est pour l'instant pas au point parce que ces IA ne font pour l'instant que du copier-coller (avec une certaine reformulation) et elles ne feront jamais plus !
mais le jour où elles auront accès à toutes les (bases de) données et avec une amélioration du contrôle de celles-ci elles sauront (re)produire le bon raisonnement dès le premier essai
et c'est pour cela qu'elles savent très bien produire du code ou des macro : elle ne font que reproduire des versions déjà produites ou quasiment ...

il avait sorti une première réponse fausse et après lui avoir fait remarqué il avait sorti la bonne réponse avec la bonne démo ...
@carpediem : Et oui. Cette conscience de l'erreur est tout à fait surprenante! Peut-être un futur où elles vont "halluciner" de véritables résultats mathématiques, comme avec ce qu'il se passe actuellement pour les images.
Je referai un contrôle l'an prochain pour voir les progrès 
J'avoue que ma suggestion (19/10 16:45) était méchante. J'espérais que mis devant une contradiction avec lui-même il se suiciderait! Du moins c'est ce qui arrive aux robots d'Assimov si on leur met le nez (ils en ont un en général) dans une contradiction interne.
Je suis déçue, il a bien vu qu'il y avait un problème et ça ne l'a pas dérangé!
C'est peu être un copié collé des travaux de notre Ramanujan, mais pourquoi l'avoir bloqué. Il me faisait tant rire...
On est pas loin d'une seconde "billion dollar mistake". Si les développeurs fainéants copient sans réfléchir du code pourri produit par une IA, il se peut qu'il fonctionne mais il y aura des bugs subtils et très dangereux dans le code de tout ce qui vous entoure. Aussi, la performance n'est pas au rendez-vous pour l'instant.
Exemple de ce que dit Bing AI (basé sur ChatGPT-4) pour
"write an efficient eratosthenes sieve in rust"
pub fn primes_up_to(upper_bound: usize) -> Vec<usize> {
let mut is_prime = vec![true; upper_bound + 1];
is_prime[0] = false;
if upper_bound >= 1 {
is_prime[1] = false
}
for num in 2..=(upper_bound as f64).sqrt() as usize {
if is_prime[num] {
let mut multiple = num * num;
while multiple <= upper_bound {
is_prime[multiple] = false;
multiple += num;
}
}
}
is_prime.iter().enumerate().filter_map(|(p, &is_p)| if is_p {Some(p)} else {None}).collect()
}
Le mot clef ici est "efficient". Le code est une implémentation bête et méchante qui prend O(n) en espace, avec une boucle for num in 2..=(upper_bound as f64).sqrt() as usize qui vérifie 2,3,4,5,6,7,... au lieu de simplement mettre 2 à part et de vérifier 3,5,7,...
Et tout à la fin, c'est anecdotique, mais il existe une fonction bool::then_some qui est faite pour ça.
Si on le guide un peu, il est vite paumé
"write a python code that efficiently picks the n-th permutation of "0123456789", using the factorial number system"
import math
def nth_permutation(input_string, n):
n -= 1 # to account for 0-based indexing
numbers = list(input_string)
permutation = ''
for i in range(len(numbers) - 1, -1, -1):
idx, n = divmod(n, math.factorial(i))
permutation += numbers.pop(idx)
return permutation
# Test the function
print(nth_permutation("0123456789", 1000000))
Et pour les maths, il y a de l'idée, mais il est à côté de la plaque
"Montre que C est algébriquement clos en utilisant le théorème de Liouville"
Le théorème de Liouville est un outil puissant pour démontrer que le corps des nombres complexes **C** est algébriquement clos, c'est-à-dire que toute équation polynomiale à coefficients complexes a une solution dans **C**.
Voici une esquisse de la preuve:
Soit **P** un polynôme non constant à coefficients complexes. On veut montrer qu'il existe un **z** dans **C** tel que **P(z) = 0**.
1. Si le degré de **P** est 1, alors **P** a clairement une racine dans **C**.
2. Supposons que le degré de **P** est **n > 1**. Alors **P** peut être écrit comme **P(z) = a_n z^n + a_{n-1} z^{n-1} + ... + a_1 z + a_0**, où **a_n ≠ 0**.
3. Considérons la fonction **f(z) = z^n + a_{n-1}/a_n z^{n-1} + ... + a_1/a_n z + a_0/a_n**. Cette fonction est holomorphe sur **C** et n'a pas de zéros à l'infini.
4. Par le théorème de Liouville, **f** est une fonction constante. Mais cela contredit le fait que **f** est un polynôme de degré **n > 1**.
5. Par conséquent, notre hypothèse initiale selon laquelle **f** n'a pas de zéros dans **C** doit être fausse. Ainsi, **P** a une racine dans **C**.
Cela démontre que **C** est algébriquement clos. Notez que cette preuve utilise une version plus forte du théorème de Liouville, qui dit que toute fonction holomorphe bornée sur **C** est constante.
Ulmiere
C'est dommage, à l'étape 3 de la preuve (pour C algébriquement clos) il suffisait de diviser par autre chose et de changer l'argument (bizarre) sur les zéros et on était bon, ça s'améliore