Bonjour,

Pour la fin, c'est du cours.
Si un point est barycentre de 2 autres, alors les 3 sont alignés.

Nicolas

J'ai oublié l'essentiel : merci de recopier ton énoncé.
C'est imposé par les règles du forum.
Un scan de livre est interdit, et même illégal.

Au moins j'ai mis un bon titre ! Enfin bref...

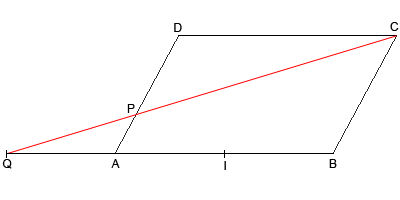
Soit ABCD un parallélogramme, P le point défini par AP = 1/3 AD et Q le symétrique du milieu I de [AB] par rapport à A.

Montrer que P = bar {(C;1),(Q;2)} et en déduire que P, Q et C sont alignés.

J'ai fait la figure:


Et même si tu me dis que pour la fin de l'exercice je dois me référé au cours (que l'on a pas encore fait), ça ne m'aide pas pour le début !

édit Océane : image insérée sur le serveur de l'

Je te propose une méthode 100 % barycentres. On va tout implement essayer d'exprimer D, I, Q et P comme barycentres de A, B et C, et voir si on peut conclure.

(a) Exprimons d'abord D comme barycentre de A, B et C, car nous en aurons besoin plus bas.
Soit O le centre du parallélogramme ABCD (intersection des diagonales).
O est le milieu de [BD] donc : D = Barycentre O,2 B,-1 (1)
Or O est le milieu de [AC] donc O,2 = Barycentre A,1 C,1
On reporte dans (1), et on obtient :
D,1 = Barycentre A,1 B,-1 C,1 (3)

(b) I est le milieu de [AB] donc I,2 = Barycentre A,1 B,1 (2)
Q est le symétrique de I par rapport à A, donc Q = Barycentre A,-2 I,1
On multiplie tous les coefficients par 2 :
Q = Barycentre A,-4 I,2
On injecte (2) par associativité des barycentres :
Q = Barycentre A,-4 A,1 B,1
Q = Barycentre A,-3 B,1
Q,2 = Barycentre A,3 B,-1 (4)

(c) AP = 1/3 AD donc P = Barycentre A,2 D,1
On utilise (3) :
P = Barycentre A,2 A,1 B,-1 C,1
P = Barycentre A,3 B,-1 C,1
On utilise (4) :
P = Barycentre Q,2 C,1

Comme tu le vois, cette méthode n'utilise que la propriété d'associativité des barycentres, et n'oblige pas à repasser par les vecteurs à un moment ou à un autre. Mais il y a d'autres façons de faire...

Nicolas