Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première LimitesTopics traitant de limites [tout]Lister tous les topics de mathématiques

1 2 +

Posté par
Doha2002re : Les limites 28-02-18 à 14:06

vham @ 24-02-2018 à 02:37

Bonjour,

En utilisant les développements limités (au programme de première ?)
quand x tend vers 0, Le numérateur est équivalent à x3/2 et le dénominateur à x3/6
la limite est donc 3.

Désolé mais j'ai bien compris.

Posté par
Doha2002re : Les limites 28-02-18 à 14:07

mgbzd

mgbzd @ 24-02-2018 à 02:58

Bonsoir,
Je ne pense pas que les développements limités soient au programme de première vham ...
Par contre Doha2002, tu peux utiliser le taux d'accroissement que tu as dû apprendre au cours de l'année.

Désolé mais on n'as pas étudié le taux d'accroissement.

Posté par
Doha2002re : Les limites 28-02-18 à 14:08

lake @ 24-02-2018 à 11:28

Bonjour,

Une solution sans utiliser la règle de l'Hopital ni les DL en admettant (c'est le gros défaut de la méthode) que les limites utilisées existent et sont finies:

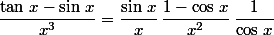
\dfrac{\tan\,x-\sin\,x}{x^3}=\dfrac{\sin\,x}{x}\,\dfrac{1-\cos\,x}{x^2}\,\dfrac{1}{\cos\,x}

d' où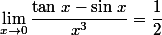 \lim\limits_{x\to 0}\dfrac{\tan\,x-\sin\,x}{x^3}=\dfrac{1}{2}

Soit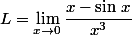 L=\lim\limits_{x\to 0}\dfrac{x-\sin\,x}{x^3} (avec les restrictions citées plus haut):

  On pose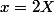 x=2X

   \dfrac{x-\sin\,x}{x^3}=\dfrac{2X-\sin\,2X}{8X^3}=\dfrac{X-\sin\,X\,\cos\,X}{4\,X^3}=\dfrac{X-\sin\,X+\sin\,X\,(1-\cos\,X)}{4\,X^3}

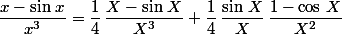
  \dfrac{x-\sin\,x}{x^3}=\dfrac{1}{4}\,\dfrac{X-\sin\,X}{X^3}+\dfrac{1}{4}\,\dfrac{\sin\,X}{X}\,\dfrac{1-\cos\,X}{X^2}

En passant à la limite en 0:

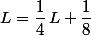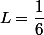
  L=\dfrac{1}{4}\,L+\dfrac{1}{8} et L=\dfrac{1}{6}

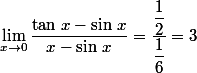
Du coup, \lim\limits_{x\to 0}\dfrac{\tan\,x-\sin\,x}{x-\sin\,x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{6}}=3

Je le répète, tout ceci est très discutable...
  

Merci mais on n'as pas ici x^3 au dénominateur!!

Posté par
Doha2002re : Les limites 28-02-18 à 14:09

matheuxmatou @ 24-02-2018 à 11:42

euh ... on est au niveau "première" là ???

Oui.

Posté par
Doha2002re : Les limites 28-02-18 à 14:10

lake @ 24-02-2018 à 11:50

Techniquement, on s'en sort avec le cours de 1ère modulo l'existence de la limite.

Il faut juste connaître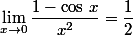 \lim\limits_{x\to 0}\dfrac{1-\cos\,x}{x^2}=\dfrac{1}{2} que certains professeurs donnent dans leur cours

Oui on a étudié ça dans notre cours.

Posté par
Doha2002re : Les limites 28-02-18 à 14:12

matheuxmatou @ 24-02-2018 à 11:50

oui parce que là... même en première S on ne fait plus de limites je crois !

Non il y a de limites.

Posté par
Doha2002re : Les limites 28-02-18 à 14:14

alb12 @ 24-02-2018 à 12:34

lake @ 24-02-2018 à 11:54

Mais c'est pour ça que j'ai proposé une démonstration (douteuse) qui ne fait appel qu'au cours de 1ère

si c'est douteux on abandonne
il y a des demos possibles mais plutot en terminale
notre posteur est surement dans une premiere mais pas en france
A lui de preciser.

Non pas en France😀.

Posté par
Doha2002re : Les limites 28-02-18 à 14:18

lake

lake @ 24-02-2018 à 12:03

Ah ben c'est sûr, avec les DL, en deux temps trois mouvements, c'est fait.

Pour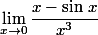 \lim\limits_{x\to 0}\dfrac{x-\sin\,x}{x^3}, on peut aussi proposer des encadrements du genre:

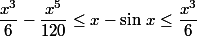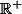   \dfrac{x^3}{6}-\dfrac{x^5}{120}\leq x-\sin\,x\leq \dfrac{x^3}{6} sur \mathbb{R}^+ avec les fonctions différences.

  puis voir sur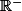 \mathbb{R}^-

Mais bon, à mon sens, c'est encore pire
lake @ 24-02-2018 à 12:03

Ah ben c'est sûr, avec les DL, en deux temps trois mouvements, c'est fait.

Pour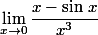 \lim\limits_{x\to 0}\dfrac{x-\sin\,x}{x^3}, on peut aussi proposer des encadrements du genre:

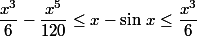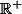   \dfrac{x^3}{6}-\dfrac{x^5}{120}\leq x-\sin\,x\leq \dfrac{x^3}{6} sur \mathbb{R}^+ avec les fonctions différences.

  puis voir sur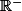 \mathbb{R}^-

Mais bon, à mon sens, c'est encore pire

Notre professeur a réglé ce prblm par l'encadrement aussi mais ça est un niveau supérieur je crois alors j'ai rien pigé de son démo.

Posté par
Doha2002re : Les limites 28-02-18 à 14:20

mgbzd @ 24-02-2018 à 19:41

Sauf qu'aujourd'hui on ne fait plus de développement limité au lycée, on ne fait pas non plus d'integrales par parties par exemple. Mais ma question est pourquoi ne pas utiliser le taux d'accroissement ?

On a ps étudié le taux d'accroissement.

Posté par
Doha2002re : Les limites 28-02-18 à 14:21

alb12

alb12 @ 25-02-2018 à 18:28

@Doha2002
Où en es-tu ?

Désolé j'ai été occupée à cause des examens.

Posté par
alb12re : Les limites 28-02-18 à 14:58

si ton prof t'a donne cet exercice c'est qu'il a traite des situations analogues.
On ne peut pas deviner la methode qu'il vous a exposee lors d'exercices similaires.

Posté par
Doha2002re : Les limites 03-03-18 à 01:39

alb12 @ 28-02-2018 à 14:58

si ton prof t'a donne cet exercice c'est qu'il a traite des situations analogues.
On ne peut pas deviner la methode qu'il vous a exposee lors d'exercices similaires.

Il nous a dit qu'on doit régler ce prblm par un encadrement lequel je sais ps.

Posté par
lakere : Les limites 03-03-18 à 10:42

Citation :
Il nous a dit qu'on doit régler ce prblm par un encadrement lequel je sais ps.


Tu n'as guère le choix:

  1)
Citation :
\dfrac{\tan\,x-\sin\,x}{x^3}=\dfrac{\sin\,x}{x}\,\dfrac{1-\cos\,x}{x^2}\,\dfrac{1}{\cos\,x}

d' où \lim\limits_{x\to 0}\dfrac{\tan\,x-\sin\,x}{x^3}=\dfrac{1}{2}


  2)
Citation :
Pour \lim\limits_{x\to 0}\dfrac{x-\sin\,x}{x^3}, on peut aussi proposer des encadrements du genre:

   \dfrac{x^3}{6}-\dfrac{x^5}{120}\leq x-\sin\,x\leq \dfrac{x^3}{6} sur \mathbb{R}^+ avec les fonctions différences.

  puis voir sur \mathbb{R}^-


  3)  \lim\limits_{x\to 0}\dfrac{\tan\,x-\sin\,x}{x-\sin\,x}=\lim\limits_{x\to 0}\dfrac{ \dfrac{\tan\,x-\sin\,x}{x^3}}{\dfrac{x-\sin\,x}{x^3}}

1 2 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !