Bonsoir flight,

comme souvent ce que tu écris n'est pas clair :
tu écris" à l'aide des entiers 1, 2 et 3 uniquement " et tu donnes des décompositions de N=5 avec 1,2,3,4.

De plus il manque des décompositions.
Pour N=4 il manque 112, 121 et 211
Pour N=5 il manque 1112, 1121, 1211 et 2111

Bonsoir,

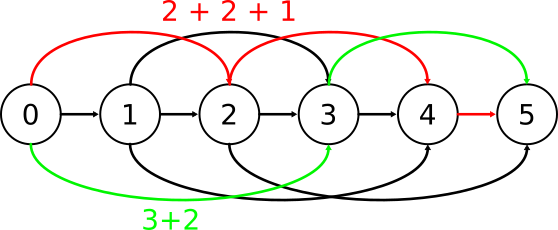
Il semble que dénombrer ces décompositions pour N revient à compter le nombre de chemins reliant 0 à N avec des branches qui sautent de 1, 2 ou 3 (voir image pour N=5).

Donc je pense qu'un algorithme type BFS (https://en.wikipedia.org/wiki/Breadth-first_search) avec un compteur incrémenté à chaque fois que le nœud N est atteint répond au problème.

Bonqoir jandri , en effet merci , j'ai pas vu ma betise
je reprend cette partie :

par exemple  pour N= 4 :

1111
1 1 2
1 2 1
2 1 1
22
31
13

exemple pour N=5

3 2
2 3
1 1 3
1 3  1
3  1  1
2  2  1
2  1  2
1  2  2
1 1 1 2
1 1 2 1
1 2 1 1
2 1 1 1
1 1 1 1 1

Bonsoir,
un algorithme récursif  fonctionne théoriquement bien

Fonction decomposition(n)
     Si n<=0 renvoyer 0 (fin)
     Si n=1 renvoyer 1 (fin)
     Sinon renvoyer decomposition(n-1)+ decomposition(n-2)+ decomposition(n-3)

Bonsoir verdurin,

c'est effectivement très facile à dérécursiver (une simple boucle suffit). On obtient instantanément :

u(1000)=275884280776648625261589241165615864513310014965269621035160184503639297891229
3462801016485671033253921841350537004356434253826361707295202024537559785200706502368
1529650477616443523167993914702739065615745008834805705605129824356815023308140687188
32813973880527601

et aussi

En fait l'algorithme précédent est faux et celui que j'ai implanté est :

Fonction decomposition(n)
     Si n<=0 renvoyer 0 (fin)
     Si n=1 renvoyer 1 (fin)
     Si n=2 renvoyer 2 (fin)
     Si n=3 renvoyer 4 (fin)
     Sinon renvoyer decomposition(n-1)+ decomposition(n-2)+ decomposition(n-3)

def nco(n):
    Liste=[0,1,2,4]
    if n<4 : return Liste[n]
    for k in range(4,n+1):
        Liste.append (Liste[k-1]+Liste[k-2]+Liste[k-3])
    return Liste[n]

Bonsoir jandri.
J'ai le même résultat pour n=1000.

Au passage le calcul pour n=50 avec le programme récursif va demander environ appels à la fonction.
On voit pourquoi ça coince.

Bonsoir

Bravo à vous deux

Un classique de dynamic programming.

Si on admet qu'il existe une décomposition pour n=0 (la décomposition sans aucun terme), l'algorithme de verdurin peu être simplifié.

def decompositions(n):
    u = [1]
    for _ in range(1, n+1):
        u.append(sum(u[-3:]))
    return u[n]

On peut même aller encore plus vite en utilisant la forme matricielle et l'exponentation rapide.


On a .

En python en utilisant numpy pour l'exponentiation rapide et decimal pour les nombres à grands exposants:

import decimal
from decimal import Decimal

import numpy
from numpy.linalg import matrix_power

decimal.getcontext().prec = 10


def decompositions(n):
    a = numpy.asarray([[Decimal(0), Decimal(1), Decimal(0)],
                       [Decimal(0), Decimal(0), Decimal(1)],
                       [Decimal(1), Decimal(1), Decimal(1)]])
    return matrix_power(a, n)[-1, -1]

Bonsoir LittleFox.
J'ai  en effet copié un mauvais résultat pour n=100.

Pour ton premier programme, en imaginant que j'ai pensé à l'indiçage u([-3: ]), j'aurais quand même commencé avec une liste à 3 éléments : on m'a gravé dans la tête que c'est un péché mortel en informatique de faire allusion à des éléments d'un tableau en dehors de la zone des indices. Mais ça marche bien.

Pour le second je me demande si l'exponentiation rapide  est plus rapide que deux additions. Toutefois il présente le grand intérêt de permettre de donner une formule close pour u(n).

Bonsoir,

l'exponentiation rapide est intéressante car c'est un algorithme en alors que la méthode naïve (pour de à faire ) est en .

Quand on passe de à le temps de calcul par la méthode naïve est multiplié par alors qu'il n'est multiplié que par avec l'exponentientation rapide.

Mais comme ici le calcul pour est instantané avec la méthode naïve et qu'on obtient déjà un nombre à chiffres je ne vois pas l'intérêt d'aller jusqu'à .

Pas si instantanée que ça. Si? Je manque quelque chose?

Pour n=10^6. La méthode naive que je donne le 18-03-24 à 10:37 mange toute ma mémoire ram avant de retourner un résultat.

En ne gardant que les 3 derniers éléments du tableau, j'ai le résultat en ~15s:

def decompositions(n):
    u, v, w = 1, 0, 0
    for _ in range(1, n + 1):
        u, v, w = u + v + w, u, v
    return u

def decompositions(n):
    a = numpy.asarray([[0, 1, 0], [0, 0, 1], [1, 1, 1]], dtype='object')
    return matrix_power(a, n)[-1, -1]

J'aurais dû être plus précis quand j'ai écrit "le calcul pour est instantané".

C'est le calcul en valeur approchée qui est instantané, le calcul en valeur exacte est beaucoup plus long car travailler avec des entiers à 100 000 chiffres est long !

On est d'accord

Il y a aussi une forme close mais elle est horrible
Elle permet de déterminer que pour n grand.