Inscription / Connexion Nouveau Sujet
Problème de volumes
Bonjour,
J'ai une exercice de géométrie qui me pose problème.
Voici l'énoncé:
Dans tout l'exercice, les unités employées sont le cm, cm² et le cm3.
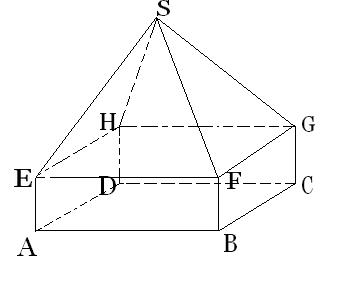
On considère le solide représenté ci-contre:
- ABCDEFGH est un pavé droit de base carrée ABCD avec AB= 1,5 et de hauteur AE = x ( où x est un nombre positif.)
- SEFGH est une pyramide régulière de hauteur 4cm
On appelle V1 le volume du solide.
1°) Démontrer que V1 = 2,25x+3
Vpyramide = 1/3 * aire de base * hauteur
Vp = 1/3 * 1.5² * 4
Vp= 3
Vpavé = Longueur * largeur * hauteur
Vpa = 1.5 * 1.5 * x
Vpa= 2.25x
V1= 2.25x+ 3
2°) Le volume V1 est-il proportionnel à la hauteur x?
On peut considérer 2.25 comem un coefficient de proportionnalité mais je ne sais pas trop comment expliquer 
3°) On considère un cylindre de révolution dont la base est un disque d'aire de 3cm² et dont la hauteur variable est notée x. On appelle V2 le volume d'un tel cylindre.
Exprimer le volume V2 en fontion de x.
V2 = 1/3 * aire de base * hauteur
V2 = 1/3 * 3 * x
V2= 1 * x
V2 = x
4°) Le volume V2 est- il proportionnel à la hauteur x?
Je pense que oui car le coefficient serait 1...
5°) Pour quelle valeur de x les deux solides ont-ils le même volume? Quel est ce volume?
2.25x + 3 = x
2.25x -x = -3
1.25x = -3
x = -2.4
Je trouve une valeur négative donc ce n'est pas possible 
Besoin d'aide SVP
Merci.
Bonjour A... Cet exercice a été traité ici même , il n'y a pas longtemps...
Mais comme le titre devait être " D.M. " ou " exo très difficile " ou " aidez-moi vite ",... cela ne va pas etre facile à retrouver !...
A la question 2, ta réponse n'est pas exacte ... S'il n'y avait que le 1er terme, le pavé, oui le volume serait proportionnel à x .
Mais comme V1 est la somme d'un volume proportionnel et d'un volume (pyramide) non proportionnel , V1 n'est pas proportionnel ...
Question 3) ... Tu vas reprendre tes calculs... auparavant, retrouve la vraie formule pour le volume du cylindre !
Donc pour le 4°) , le volume est proportionnel à la hauteur car le coefficient de proportionalité est 3.
Pour le 5°),
3x = 2.25x+ 3
3x - 2.25x = 3
0.75x = 3
x = 3/0.75
x = 4
C'est bien ça ? :d
Merci
C'est tout-à-fait cela ...
Pour la question 4), il vaudrait peut etre mieux dire :
Le volume est proportionnel à la hauteur, et le coefficient de proportionnalité est 3 .
Merci 
Et donc pour trouver le volume il suffit de remplacer x par 4 dans les deux expressions.
Le volume est donc de 12 cm3.
Merci de votre aide.
Bonne journée à jacqlouis et lucillda.



