Inscription / Connexion Nouveau Sujet
utilisation d une methode a regression lineaire
bonjour
j'ai comme données pour les années 2002,2003 ,2004 et 2005 le nombre d'enfants ayant 2 ans dans une région.
puis je utiliser une methode de regression lineaire (la formule prevision dans excel) pour prévoir le nombre d'enfants que j'aurai pour les années 2006 à 2011?
merci
Bonjour,
il faut auparavant t'assurer que les données pour [2002-2005] sont effectivement sur une droite.
Sinon extrapoler par une fonction polynome si ce n'est pas le cas
Par ailleurs, et ce n'est pas une question de pure mathématique, il faut/faudrait aussi tenir compte d'autres facteurs qui pourraient influer :
- exode d'une région prévue à une date donnée, par exemple,
- au contraire, implantation de de nlles industries => afflux de (jeunes) personnes/couple dans la région => natalité => enfants de 2 ans en 20xx
Philoux
Quelles sont tes valeurs pour 2002-2005 ?
2002:7305
2003:7020
2004:6910
2005:6845
c'est pas vraiment sur une droite....
En linéaire : ceci
mal adapté : coff = -0,946
La suite arrive
Philoux
Philoux, tu dis : "mal adapté : coff = -0,946"
|coeff| est proche de 1 => la régression linéaire est adaptée, non ?
Nicolas
euuh je peux utiliser cette methode pour faire mes previsions alors ?
Nicolas_75
Celles que j'avais bien adaptées avaient un coeff >0.99
maintanat, en démographie, ils peuvent peut-être se satisfaire de 0.94...
Si des spécialistes peuvent infirmer/confirmer
Philoux
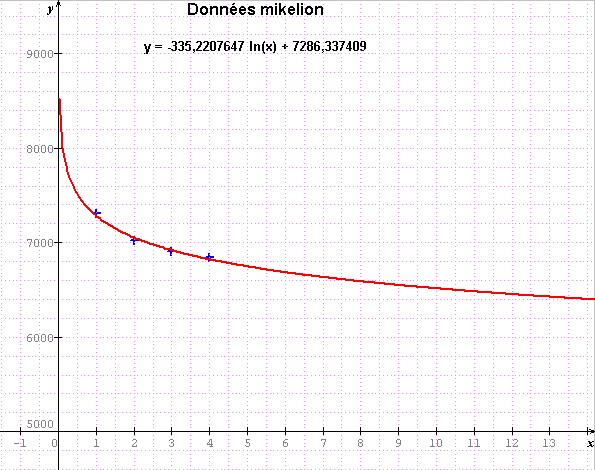
ci joint, régression logarithmique pour un coeff de 0.9914
Malentendu de ma part : je pensais (à tort) que tu étais inquiet de voir un nombre négatif.  Désolé.
Désolé.
Quant à la limite entre 0,95 et 0,99 : c'est une question de degré de tolérance. De toute façon, avec seulement 4 données, on ne peut pas conclure grand chose dans le monde réel à mon avis. 
Nicolas
on vient de me transmettre d'autres données:
1999:6890
2000:6917
2001:7060
2002:7305
2003:7020
2004:6910
2005:6845
2006:6783
donc pas tres lineaire.
remarque: philou tu lui donnes un tube, il te fait une voiture !!!
merci
Effectivement, Nicolas_75
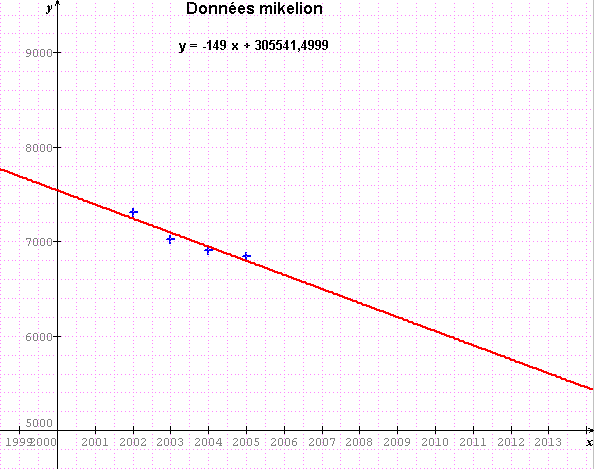
mais c'est surtout la tendance qui risque d'être erronée
la régression linéaire décroit plus fortement que celle logarithmique...
Philoux
>mike
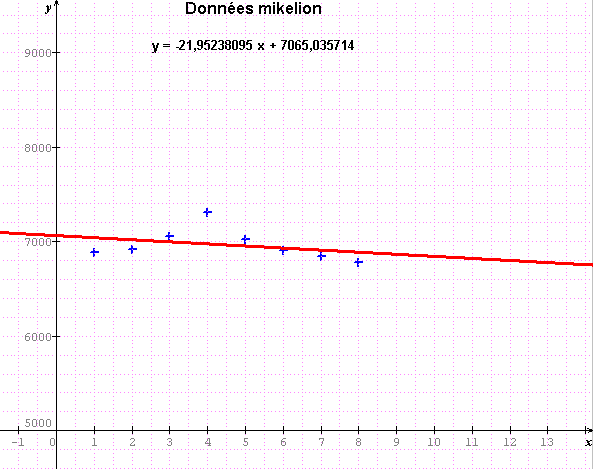
c'est encore plus flagrant avec un coeff de 0.32
manifestement, tu as un changement de situation en 2002 : croissance puis décroissance
Tu as intére^t à faire ta courbe à partir de 2002, sans tenir compte des données antérieures
et à expliquer la raison de ce changement (pour voir si ca peut être cyclique, si ca peut revenir ?
Philoux
sinon personne ne connait une autre methode de prevision que je pourrai utiliser ?
Salut!
Le monde de l'estimation est souvent cruel...
Le probleme ici, c'est que manifestement ton phenomene est soumis a des "accidents".
Deux options:
1)le phenomene perturbateur est intrinseque au phenomene observe (il fait partie de l'etude, quoi). Ben zut. Il faut trouver un bon modele. La c'est pas de la tarte: il faudrait faire des suppositions sur la peridodicite de la chose, son amplitude, etc...
2) le phenomene perturbateur est explicable a partir de donnees exterieures. Soit on le modelise a part, et on regarde quelle est son influence ensuite, soit on "triche". Par exemple, on pourrait envisager de supprimer la donnee "2002" sou spretexte qu'elle est vraiment hors-norme.
Lorsqu'on fait de l'estimation dans des cas difficiles (quand on n'a pas de regression lineaire evidente, et encore...), le travail ne consiste pas a trouver "la bonne methode de prevision". Le travail consiste a la construire... Pour cela il faut faire des choix, notamment des choix de modele, que l'on justifie a priori par des hypotheses sur le comportement du phenomene (lois physiques, donnees externes, etc...), et ensuite a posteriori en regardant ce que donnerait le modele sur des donnees connues.
Les mathematiques ne deviennent qu'un simple outil calculatoire, l'essentiel est fait lors des choix de construction du modele.
Foin de la "philosophie" de l'estimation (je renvoie les amateurs a des ouvrages specialises - dans l'estimation, pas dans la philosophie -), et revenons au probleme...
Personnellement, je ferais comme Philoux: on ignore les donnees anterieures a 2002 (a cause de la 'cassure' qui revele un changement radical de comportement, et pas juste une simple anomalie). On suppose que les conditions qui regissent le phenomene vont perdurer (deja, la... on ne dit pas quelles sont ces conditions...). Et on fait une regression (lineaire ou log, a toi de voir: tu n'aurais pas d'autres donnees - sur autre chose- que tu pourrais correler?).
Il faut quand meme garder a l'esprit que faire une prevision sur 4-5 ans a partir de tes donnees, c'est un peu temeraire...
Courage,
biondo
Bonjour,
Apparemment, tu es face à un vrai problème apparu dans une étude, pas un exercice de maths théorique.
Dans ces conditions, la première étape est, me semble-t-il, ton analyse sur les données et les phénomènes sous-jacents, pour déterminer quel est le bon modèle.
Regarde le graphe de philoux 14h57 :
- penses-tu que 2002 est un "pic" qui sépare les données en deux parties symétriques ("avant" et "après") ? Dans ce cas, on peut approximer les données par une courbe en "cloche". (Mais cela me semble absurde sur le plan démographique.)
- penses-tu, comme le propose philoux, que le modèle a changé en 2002, et que les données suivent une autre loi d'évolution (inconnue) à partir de cette date ? Dans ce cas, il ne faut prendre en compte que les données postérieures à 2002 et approximer par une droite ou un logarithme.
- penses-tu que l'évolution est périodique, et qu'un nouveau pic apparaitra dans x années ? On peut alors approcher par une fonction périodique.
Etc...
A mon sens, sur cet exemple, les mathématiques doivent être au service de ton analyse. Ce ne sont pas les maths qui te donneront le "résultat".
Ce n'est que mon avis.
Cordialement,
Nicolas
Bonjour,
Tout à fait d'accord avec les explications de biondo et Nicolas_75.
>Mike
Ce que tu peux également faire, c'est regarder ce qui se passe dans d'autres régions et tenter de connaître/justifier ce changement de comportement avant/après 2002.
Ici aussi, c'est donc plus de l'analyse démographique (il me semble qu'il y a des cadors sur l'île à ce propos, je pense à enzo et d'autres) que de la nature de l'outil mathématique à utiliser.
Prendre le bon outil (comme en mécanique d'ailleurs) nécessite de savoir sur quoi on veut l'utiliser (nature des données 1999-2006 ou 2002-2005) et ce que l'on veut faire (montrer la poursuite de la décroissance ou une remontée des effectifs).
Si tu avais pris une extrapolation polynomiale de d° 2, tu aurais une remontée des effectifs avec les données 2002-2005.
Bon courage
Philoux
waoow ca philisophe vachement aujourd'hui ?
le pire c'est que j'ai fait plein de stats il y a longtemps et que je ne me rappelle plus de grand chose...
le philoux il utiliserait quoi comme logiciel pour faire les graphes qu'il a mis ?
bon en tous cas merci a tous.
Salut mike,
il utiliserait quoi comme logiciel pour faire les graphes :
![]() Logiciel de calcul de surface
Logiciel de calcul de surface
Philoux
Bonjour tout le monde  ,
,
Ton problème mikelion est plus lié à l'étude des séries chronologiques qu'à la régression linéaire.
Malheureusement, et la remarque a été faite, tu disposes de peu de données...
Tu peux utiliser un "mix" des deux en calculant un modèle qu'on appelle auto-régressif, autrement dit calculer une équation de la forme:
Yt = a Yt-1 + 
Le coefficient "a" peut se déterminer par régression linéaire.
Un bon moyen serait d'avoir le détail des ces naissances, par exemple, non pas les chiffres par année mais par mois ou trimestres.
Enfin, les techniques de lissage exponentiel peuvent aussi être très intéressantes, dans la mesure où elles ont pour but d'accorder plus de poids aux observations récentes qu'aux observations passées.



 statistiques en Bts
statistiques en Bts