Fiche de mathématiques
Ile mathématiques > maths 1ère > Trigonométrie : pour aller plus loin
Comparons les mesures des angles)
et )
.
1. Exprimer à l'aide des angles )
et )
.
2. Comparer et )
d'une part et et )
d'autre part.
3.Comparer alors et .
1. Comparer)
et )
.
2. Démontrer à l'aide de l'égalité : + (\overrightarrow{\text{CB}},\overrightarrow{\text{CA}}) + (\overrightarrow{\text{AC}},\overrightarrow{\text{AB}}) = \pi)
les égalités : = (\overrightarrow{\text{BA}},\overrightarrow{\text{BC}}) + (\overrightarrow{\text{CB}},\overrightarrow{\text{CA}}))
et
 = 2 (\overrightarrow{\text{BA}},\overrightarrow{\text{BC}}))
.
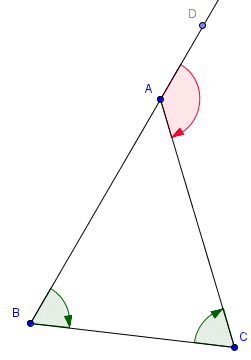
[Sur la figure,![(\overrightarrow{\text{AD}},\overrightarrow{\text{AC}}) = 2 (\overrightarrow{\text{BA}},\overrightarrow{\text{BC}})]](https://latex.ilemaths.net/latex-0.tex?(\overrightarrow{\text{AD}},\overrightarrow{\text{AC}}) = 2 (\overrightarrow{\text{BA}},\overrightarrow{\text{BC}})])
)
de centre O et D le point diamétralement opposé à A sur .
1. Démontrer que = 2 (\overrightarrow{\text{AB}},\overrightarrow{\text{AO}}))
.
2. Démontrer que = 2 (\overrightarrow{\text{AB}},\overrightarrow{\text{AC}}))
.
Cette dernière relation généralise une propriété utilisée au collège : l'angle au centre est double de l'angle inscrit interceptant le même arc de cercle.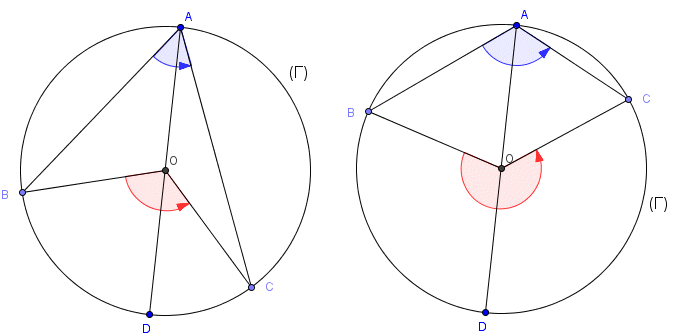
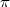radians :
 + (\overrightarrow{BC};\overrightarrow{BA}) + (\overrightarrow{CA};\overrightarrow{CB}) = \pi)
Donc :
 = \pi - (\overrightarrow{AB};\overrightarrow{AC}) - (\overrightarrow{BC};\overrightarrow{BA}))
 = \pi - (\overrightarrow{AB};\overrightarrow{AC}) + (\overrightarrow{BA};\overrightarrow{BC})})
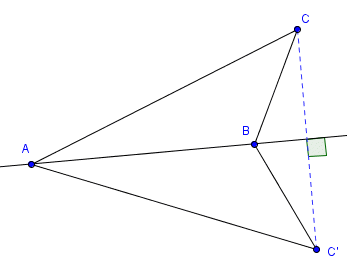
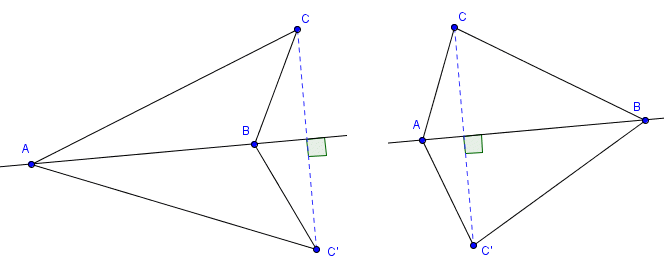
2. La droite (AB) est la médiatrice du segment [CC'] donc les triangles ACC' et BCC' sont isocèles respectivement en A et en B.
On en déduit que :
 = - (\overrightarrow{AB};\overrightarrow{AC'})})
et  = - (\overrightarrow{BA};\overrightarrow{BC'})})
3. En substituant les résultats obtenus à la question 2 dans l'expression obtenue à la question 1, on obtient :
 = \pi - (\overrightarrow{AB};\overrightarrow{AC}) + (\overrightarrow{BA};\overrightarrow{BC}))
 = \pi + (\overrightarrow{AB};\overrightarrow{AC'}) - (\overrightarrow{BA};\overrightarrow{BC'}))
Or, on a : = (\overrightarrow{u};\overrightarrow{v}))
donc :  = (\overrightarrow{AB};\overrightarrow{C'B}))
 = \pi + (\overrightarrow{AB};\overrightarrow{AC'}) - (\overrightarrow{AB};\overrightarrow{C'B}))
Or, on a : = \pi - (\overrightarrow{u};\overrightarrow{v}))
donc :  = \pi - (\overrightarrow{C'A};\overrightarrow{AB}))
 = \pi + \pi (\overrightarrow{C'A};\overrightarrow{AB}) - (\overrightarrow{AB};\overrightarrow{C'B}))
![(\overrightarrow{CA};\overrightarrow{CB}) = 2\pi - \left[ (\overrightarrow{C'A};\overrightarrow{AB}) + (\overrightarrow{AB};\overrightarrow{C'B})\right]](https://latex.ilemaths.net/latex-0.tex?(\overrightarrow{CA};\overrightarrow{CB}) = 2\pi - \left[ (\overrightarrow{C'A};\overrightarrow{AB}) + (\overrightarrow{AB};\overrightarrow{C'B})\right])
En supprimant le 2 (un tour complet), et en utilisant la relation de Chasles, on obtient finalement :
 = - (\overrightarrow{C'A};\overrightarrow{C'B}) })
Remarque : Les méthodes ci-dessus restent valables quel que soit la position du point C par rapport aux points A et B.
 = (\overrightarrow{CA};\overrightarrow{CB}))
donc  = -(\overrightarrow{CB};\overrightarrow{CA})} \;\;\; (1))
2. Dans le triangle ABC, la somme des angles étant égale à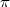 radians, on a :
 + (\overrightarrow{CB};\overrightarrow{CA}) + (\overrightarrow{AC};\overrightarrow{AB}) = \pi)
Donc :
 = \pi - (\overrightarrow{BA};\overrightarrow{BC}) - (\overrightarrow{CB};\overrightarrow{CA}))
Or, on a : donc :
![(\overrightarrow{BA};\overrightarrow{AC}) = \pi - (\overrightarrow{AC};\overrightarrow{AB})\\ (\overrightarrow{BA};\overrightarrow{AC}) = \pi - \left[ \pi - (\overrightarrow{BA};\overrightarrow{BC}) - (\overrightarrow{CB};\overrightarrow{CA}) \right]\\ \fbox{(\overrightarrow{BA};\overrightarrow{AC}) = (\overrightarrow{BA};\overrightarrow{BC}) + (\overrightarrow{CB};\overrightarrow{CA})} \;\;\; (2)](https://latex.ilemaths.net/latex-0.tex?(\overrightarrow{BA};\overrightarrow{AC}) = \pi - (\overrightarrow{AC};\overrightarrow{AB})\\ (\overrightarrow{BA};\overrightarrow{AC}) = \pi - \left[ \pi - (\overrightarrow{BA};\overrightarrow{BC}) - (\overrightarrow{CB};\overrightarrow{CA}) \right]\\ \fbox{(\overrightarrow{BA};\overrightarrow{AC}) = (\overrightarrow{BA};\overrightarrow{BC}) + (\overrightarrow{CB};\overrightarrow{CA})} \;\;\; (2))
D'après l'égalité (1) démontrée à la question précédente, on a :
 = -(\overrightarrow{BC};\overrightarrow{BA}) = (\overrightarrow{BA};\overrightarrow{BC}))
Et donc, en utilisant cette égalité dans la relation (2), on obtient bien :
 = 2 (\overrightarrow{BA};\overrightarrow{BC})} )
Remarque :
Les vecteurs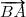
et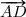 
ayant même direction et même sens, on a  = (\overrightarrow{AD};\overrightarrow{AC}) )
d'où le résultat proposé à la fin de l'exercice.
On a : = \pi)
En décomposant avec la relation de Chasles, on obtient :
 + (\overrightarrow{OB};\overrightarrow{OD}) = \pi)
Donc : = \pi - (\overrightarrow{OA};\overrightarrow{OB}))
Le triangle ABO étant isocèle en O, on a : = \pi - 2 (\overrightarrow{AB};\overrightarrow{AO}))
En utilisant ce résultat avec la relation précédente, on obtient finalement :
![(\overrightarrow{OB};\overrightarrow{OD}) = \pi - \left[ \pi - 2 (\overrightarrow{AB};\overrightarrow{AO}) \right] \\ \fbox{(\overrightarrow{OB};\overrightarrow{OD}) = 2 (\overrightarrow{AB};\overrightarrow{AO}) }](https://latex.ilemaths.net/latex-0.tex?(\overrightarrow{OB};\overrightarrow{OD}) = \pi - \left[ \pi - 2 (\overrightarrow{AB};\overrightarrow{AO}) \right] \\ \fbox{(\overrightarrow{OB};\overrightarrow{OD}) = 2 (\overrightarrow{AB};\overrightarrow{AO}) } )
MÉTHODE 2
Le triangle ABD est inscrit dans le demi-cercle de diamètre [AD] donc ABD rectangle en B, on en tire :
 = \dfrac{\pi}{2})
En décomposant avec la relation de Chasles, on obtient :
 + (\overrightarrow{BO};\overrightarrow{BA})= \dfrac{\pi}{2}\\ (\overrightarrow{BD};\overrightarrow{BO}) = \dfrac{\pi}{2} - (\overrightarrow{BO};\overrightarrow{BA}))
Or le triangle ABC est isocèle en O, donc = (\overrightarrow{AB};\overrightarrow{AO}))
, ce qui donne :
 = \dfrac{\pi}{2} - (\overrightarrow{AB};\overrightarrow{AO}))
Le triangle BDO est isocèle en O, donc :
![(\overrightarrow{OB};\overrightarrow{OD}) = \pi - 2(\overrightarrow{BD};\overrightarrow{BO})\\ (\overrightarrow{OB};\overrightarrow{OD}) = \pi - 2 \left[ \dfrac{\pi}{2} - (\overrightarrow{AB};\overrightarrow{AO}) \right] \\ \fbox{(\overrightarrow{OB};\overrightarrow{OD}) = 2(\overrightarrow{AB};\overrightarrow{AO})}](https://latex.ilemaths.net/latex-0.tex?(\overrightarrow{OB};\overrightarrow{OD}) = \pi - 2(\overrightarrow{BD};\overrightarrow{BO})\\ (\overrightarrow{OB};\overrightarrow{OD}) = \pi - 2 \left[ \dfrac{\pi}{2} - (\overrightarrow{AB};\overrightarrow{AO}) \right] \\ \fbox{(\overrightarrow{OB};\overrightarrow{OD}) = 2(\overrightarrow{AB};\overrightarrow{AO})})
2. On démontre de la même manière : = 2(\overrightarrow{AO};\overrightarrow{AC}))
.
Donc :
![(\overrightarrow{OB};\overrightarrow{OC}) = (\overrightarrow{OB};\overrightarrow{OD}) + (\overrightarrow{OD};\overrightarrow{OC})\\ (\overrightarrow{OB};\overrightarrow{OC}) = 2 (\overrightarrow{AB};\overrightarrow{AO}) + 2(\overrightarrow{AO};\overrightarrow{AC})\\ (\overrightarrow{OB};\overrightarrow{OC}) = 2 \left[ (\overrightarrow{AB};\overrightarrow{AO}) + (\overrightarrow{AO};\overrightarrow{AC}) \right]\\ \fbox{(\overrightarrow{OB};\overrightarrow{OC}) = 2(\overrightarrow{AB};\overrightarrow{AC})}](https://latex.ilemaths.net/latex-0.tex?(\overrightarrow{OB};\overrightarrow{OC}) = (\overrightarrow{OB};\overrightarrow{OD}) + (\overrightarrow{OD};\overrightarrow{OC})\\ (\overrightarrow{OB};\overrightarrow{OC}) = 2 (\overrightarrow{AB};\overrightarrow{AO}) + 2(\overrightarrow{AO};\overrightarrow{AC})\\ (\overrightarrow{OB};\overrightarrow{OC}) = 2 \left[ (\overrightarrow{AB};\overrightarrow{AO}) + (\overrightarrow{AO};\overrightarrow{AC}) \right]\\ \fbox{(\overrightarrow{OB};\overrightarrow{OC}) = 2(\overrightarrow{AB};\overrightarrow{AC})})
Publié par Tom_Pascal
le
Réflexions et mesures d'angles de vecteurs
Complétons à l'aide des angles orientés de vecteurs, la relation déjà rencontrée entre les angles au centre et les angles inscrits interceptant le même arc dans un cercle.
exercice 1
Soit (AB) une droite, C un point n'appartenant pas à (AB), C' le symétrique de C par rapport à (AB).Comparons les mesures des angles
1. Exprimer
2. Comparer
3.Comparer alors
exercice 2
Soit ABC un triangle isocèle, AB = AC.1. Comparer
2. Démontrer à l'aide de l'égalité :
les égalités :
[Sur la figure,
exercice 3
Soit A,B,C trois points d'un cercle1. Démontrer que
2. Démontrer que
Cette dernière relation généralise une propriété utilisée au collège : l'angle au centre est double de l'angle inscrit interceptant le même arc de cercle.
exercice 1
1. Dans le triangle ABC, la somme des angles est égale àDonc :
2. La droite (AB) est la médiatrice du segment [CC'] donc les triangles ACC' et BCC' sont isocèles respectivement en A et en B.
On en déduit que :
3. En substituant les résultats obtenus à la question 2 dans l'expression obtenue à la question 1, on obtient :
Or, on a :
Or, on a :
En supprimant le 2
Remarque : Les méthodes ci-dessus restent valables quel que soit la position du point C par rapport aux points A et B.
exercice 2
1. Les angles à la base d'un triangle isocèle sont égaux donc :2. Dans le triangle ABC, la somme des angles étant égale à
Donc :
Or, on a :
D'après l'égalité (1) démontrée à la question précédente, on a :
Et donc, en utilisant cette égalité dans la relation (2), on obtient bien :
Remarque :
Les vecteurs
exercice 3
1. MÉTHODE 1On a :
En décomposant avec la relation de Chasles, on obtient :
Donc :
Le triangle ABO étant isocèle en O, on a :
En utilisant ce résultat avec la relation précédente, on obtient finalement :
MÉTHODE 2
Le triangle ABD est inscrit dans le demi-cercle de diamètre [AD] donc ABD rectangle en B, on en tire :
En décomposant avec la relation de Chasles, on obtient :
Or le triangle ABC est isocèle en O, donc
Le triangle BDO est isocèle en O, donc :
2. On démontre de la même manière :
Donc :
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Voir la correction
forum de première