Inscription / Connexion Nouveau Sujet
1 plan, 2 cercles, 1 distance, 1 tangente et 2 coordonnées
bonjour à tous.
je suis graphiste et je fais un peu de programmation. je viens vous demander votre aide.
j'aurais besoin de trouver les coordonnées de deux points (a et b) en fonction de la tangente commune de deux cercles et de leur distance.
d'avance merci
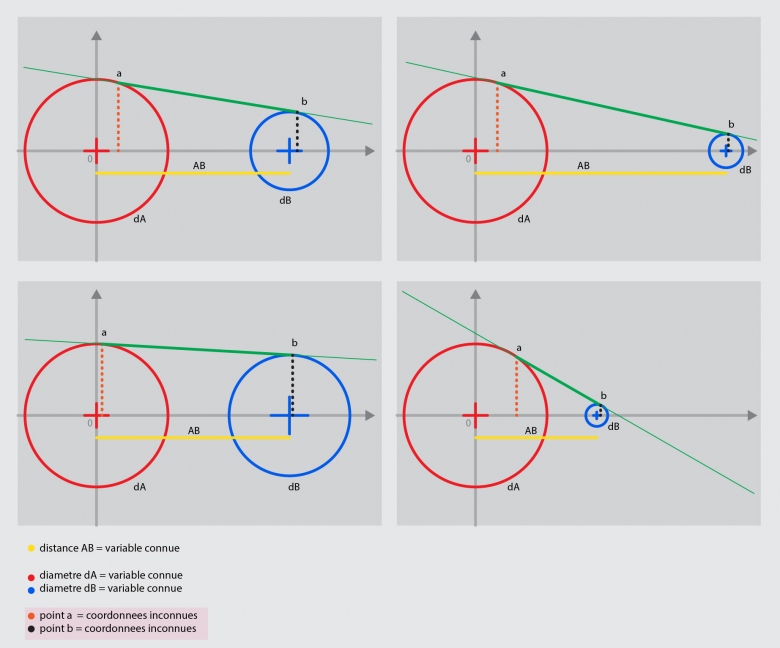
J'ai la flemme de faire les calculs, mais voici le début.
Sur ta configuration, il y a un point essentiel, c'est le point d'intersection entre la droite verte et la droite AB. On le voit uniquement sur le 4ème exemple.
Il faut trouver les coordonnées de ce point (par Thales) ; Notons le C.
Ensuite, on va dire : le triangle AaC est rectangle en a, ce qui va nous donner les coordonnées de a.
et idem pour le triangle BbC.
heu leur tangente commune ... je m'exprime sans doute très mal. je suis un profane.
en fait:
- j'ai deux cercles:
- un aux coordonees 0,0 (le rouge)
- un autre qui ne bouge qu'en x (le bleu)
- les deux sont de tailles variables.
et j'aimerais trouver une solution qui me permette d'avoir les coordonnees des deux points (a et b) d'une tangente qui toucherait les deux cercles.
merci, ça me permet d'avancer. mais c'est je ne peux determiner O [puisque je ne peux pas tracer], du fait je ne peux obtenir E.
je ne comprends pas bien ce que tu cherches, les coordonnees des points de tangence en fonction des rayons et de la distance entre les deux centres ?
J'ai fait un calcul rapide (logiciel) qui semble donner:
j'appelle r1 et r2 les rayons et d la distance
A confirmer (script non relu) !
Bonjour,
Si l'on appelle C le point de concours de la tangente commune avec l'axe des centres, le grand cercle est le transformé du petit dans l'homothétie de centre C et de rapport r1/r2.
On en déduit facilement que CO=d*r1/(r1-r2).
Soit  , l'angle (OC, Oa), alors cos
, l'angle (OC, Oa), alors cos =r1/CO
=r1/CO
puis les coordonnées (r1cos , r1sin
, r1sin ) pour a
) pour a
(r2 cos , r2 sin
, r2 sin ) pour b
) pour b
En développant, on retrouve bien les formules données par le logiciel.
sublime ! merci merci merci. je ne vous raconte pas de quel état d'euphorie je suis.
c'est exactement ce que je voulais. la formule traduite python donne ceci.
((math.pow(d,2)+r1*r2-math.pow(r2,2))/d), ((r2* math.sqrt(math.pow(d,2)-math.pow(r1,2)+2*r1*r2-math.pow(r2,2)))/d)
((math.pow(r1,2)-r1*r2)/d), (r1*math.sqrt(math.pow(d,2)-math.pow(r1,2)+2*r1*r2-math.pow(r2,2))/d)
encore merci
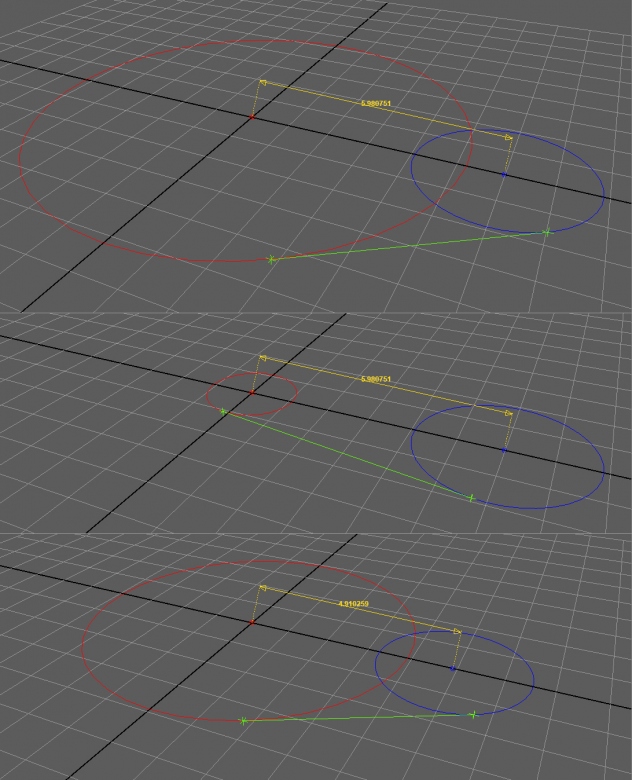
Parfait. J'en profite quand même pour corriger un oubli. Les coordonnées de b sont
(d+r2 cos , r2 sin
, r2 sin )
)
Mais alb12 avait déjà tout dit.
Pour info ci dessous le script à executer dans un ecran de geometrie 2d du logiciel libre/gratuit Xcas
(on couple la geometrie dynamique et le calcul formel)
puis les commandes renvoyant les coordonnees des points de tangence
supposons(r1=[1,0,1,0.01]);
C1:=cercle(0,r1);
supposons(r2=[0.53,0,1,0.01]);
supposons(d=[2.5,0,10,0.1]);
C2:=cercle(d,r2);
D:=droite(i*r1,d+i*r2);
A:=inter_unique(D,droite(y=0));
C:=cercle(d,A);
M:=inter_unique(C,C2);
N:=inter_unique(droite(A,M),C1);
simplifier(coordonnees(M))
simplifier(coordonnees(N))



 géométrie en post-bac
géométrie en post-bac