Inscription / Connexion Nouveau Sujet
Aire d'un pentagone regulier
bonjour =) ,
Enoncé:
Piero Della Francesca, peintre et ami de Léonard de Vinci, avait une formule pour calculer l'aire d'un pentagone régulier :
" le produit des 5/8 du diamètre par la diagonale "
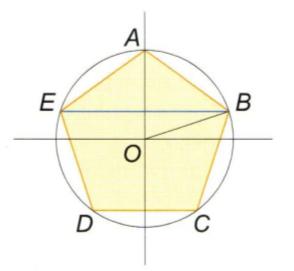
Démontrer cette formule ( la "diagonale" es BE, le diamètre est celui du cercle (j'ai trouvé 2 OB) )
j'ai un problème sur la phrase de Piero , je n'arrive pas a comprendre quand il dit " par la diagonale" :s
pouvez vous m'aider svp
merci d'avance
bonsoir,
l'aire cherchée est égale à 5 fois celle du triangle OBA puisque le pentagone est régulier
je note H l'intersection de BE et OA,BH est perpendiculaire à AO
aire triangle AOB=(AOxBH)/2= (RxBE)/4=(DxBE)/8
donc l'aire du pentagone régulier est:5(DxBE)/8=(5/8)(DxBE)
c'est bien les 5/8 du produit du diametre D par BE
rebonsoir,
je ne comprends pas pourquoi AO = R dans (AOxBH)/2 = (RxBE)/4
parce que tout est multiplié par 2 alors pourquoi pas le AO aussi? o.Ô
bonsoir,
AO c'est bien le rayon du cercle A0=B0 =R=D/2 c'est la distance de A qui est sur le cercle au centre du cercle
BE=2BH les points B et E sont symétriques par rapport à la droite AO
AOx(BH)/2=AOx(BE/4)=(D/2)x(BE/4)=(DxBE)/(2x4)=(DxBE)/8
Annuler
connectez vous