As-tu bien fait la figure ?
Comment y sont orientés le plan Fb et les segments HD, DE et EF par rapport au trièdre O, i, j, k ?

Bonjour, merci de m'aider.
Oui, c'est bon j'ai fait la figure.
Mais je suis bloqué à la b)(2eme question): "Exprimer son aire en fonction de b"
J'ai déja trouvé [DE] : 2b
Mais je n'arrive pas à exprimer HD ou FE en fonction de b pour calculer l'aire du rectangle.
Merci

HD peut cependant être déterminé dans le triangle AOS.

Merci pour l'indication !

Pour la suivante, G a pour coordonnées (x;y;..)
Je ne vois pas comment exprimer z_G
merci

zG peut être calculé dans le triangle BOS.

Oui, j'y ai pensé, mais je n'arrive pas à exprimer BG
Je pose W milieu de DE
et j'arrive à BG=GW

Pourquoi n'utilises-tu pas OW et OB ?

Merci, ça m'a aidé ...
Je trouve 1-b
Est-ce bon ?

Pour WG, mon résultat est un peu différent.

Et bien pourtant :
WG=(SOBW)/BO
Or BW=1-b et SO=BO=1

Mais BW n'est pas égal à  1 - b  ni BO égal à 1 !

Oui, une petite erreur :
BO=2
BW=2 -b

WG=((2)-b)/2

BW ???

Oui, que trouves tu pour BW ?

BW = V2 - b/V2.

voici mon raisonnement :
BW/BO=WG/SO
WG=(SOBW)/BO
Or SO=1
BO=2
BW=2-b

Donc :
WG=((2)-b)/2

BW = V2 - b : faux.

En fait, je pensais jusqu'a présent que b correspondait à OW,
comme sur le schéma en bas. C'est pour ça que j'ai dit plus haut que DE=2b et que BW = 2 - b
A quoi correspond t-il en réalité ?
Merci

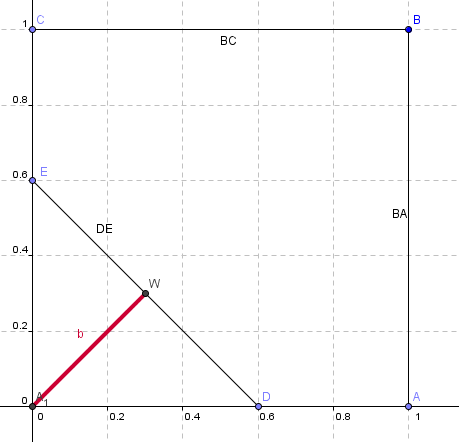
L'équation de la droite ED est  x + y = b.
Si x = 0, y = b.
b  est l'ordonnée du point E (ou, aussi bien, l'abscisse du point D).

Merci beaucoup !
j'ai compris, je vais refaire mes calculs.

Voici mes résultats :

b)Exprimer l'aire du rectangle en fonction de b
  DE=b2
  HD=1-b
ensuite je calcul l'aire

c) On a G(;;)
Je pense que c'est correct, et toi qu'en penses-tu ?
Merci

C'est correct sauf la cote de G.

Pourquoi ?

Je trouve  zG = 1 - b/2.

Pourtant, je ne trouve pas d'erreur dans mon calcul :
WG=(BWOS)/BO  =      =       =  

Bonne soirée

OW est égal à  b/V2  et non à  b/2.

Bonne soirée à toi aussi.

Merci beaucoup,
Je trouve maintenant comme toi,
Je vais essayer la suite.

Pour la d)
J' ai calculé les coordonnées de F et H
et j'ai donc trouvé les coordonnées de L (milieu de FH) : (b/2;b/2;bV2)

J'ai calculé la distance GL :8b²-4bV2+1

De plus HL=(bV2)/2

Donc l'aire du triangle : :8b³(V2/2) -4b² + (bV2)/2

A_sb : 8b³V2/2 -4b² + (bV2)/2 +bV2 - b²V2
                   =b³4V2 + b²(-4-V2) + b(3V2)/2

Es-tu d'accord avec moi ?

Pour la 2) je pense étudier la dérivée et faire un tableau de signe et de variation pour voir la valeur de b pour laquelle l'aire est maximale.

Je te remercie pour ton aide

A la fin du c), on demande l'aire du triangle FGH.
Au d), je présume que l'aire A_s(b) demandée est celle de la section de la pyramide par le plan P_b.
Qu'as-tu cherché à calculer ?
Pour GL, cela me paraît plus simple :  GL = GW - LW = 1 - b/2 - (1 - b) = b/2.

A la question 1), on nous demandait de déterminer la nature de la section
C'est un pentagone,
Et à la question d) on nous demande l'aire de la section,
donc pour moi, c'est l'aire du pentagone.
Je l'ai recalculée (car il y avait une erreur)
En effet, ta methode est plus simple.
Je trouve A_s(b)= (b²V2)/4 + bV2 - b²V2
Je vais donc étudier cette fonction pour trouver le maximum

J'en profite pour te poser la dernière question car le DM est à rendre pour demain :

Démontrer que parmi les plans P_b, celui dont la
section a une aire maximale est le plan de vecteur directeur
et passant par G.

G :centre de gravité de OAC.

Merci beaucoup

C'est bon, je trouve que pour b=2/3, l'aire est maximale

As-tu une idée pour la suivante ?

Le plan donnant l'aire maximale a donc pour équation  x + y = 2/3.
Je ne comprends pas cette dernière question.

Moi non plus je ne comprend pas cette question.
Mais je vais continué à cherché.

oups, "continuer à chercher"

tant pis, c'est pas grave...
Je te remercie pour ton aide
a+