il s'agit d'un programme de résolution de l'équation f(x)=0 dans l'intervalle entre 0 et 1. La méthode de la recherche de solution est appelée la dichotomie : on coupe l'intervalle en 2 et on vérifie dans quelle portion se trouve la solution.

il faut au préalable saisir la fonction f dans Y1:=cos(2X)-X

Et voici le programme :

input P
0->A
1->B
While B-A>P
(A+B)/2->M
if Y1(M)>0
M->A
else
M->B
End
End
Disp A
Disp B

Oui ma professeur de maths m'a parlé de cette méthode

j'ai entré l'algorithme dans ma calculatrice il ne marche toujours pas et affiche une erreur au niveau du "ELSE"..

Au final, il suffisait tout simplement de supprimer le "ELSE"
Mais je n'ai pas compris à quoi servait cet algorithme ?

cet algorithme recherche une solution entre 0 et 1 pour l'équation f(x)=0
c'est à dire cos(2x)-x =0
et donc cos(2x) = x

la solution est une valeur égale au cosinus du double de cette valeur.

Bonjour,

supprimer le else ne marchera pas (l'algorithme ne sortira pas d'erreur de syntaxe mais donnera un résultat aberrant)
il faut voir en regardant la doc de la calculette comment exactement on écrit un "if ... else"
peut être faut-il lui dire que la partie "if" est terminée ou va savoir quel "gadget" d'écriture pour lui dire que l'on veut réellement ce else.

la méthode de dichotomie est basée sur le TVI (théorème des valeurs intermédiaires)
si f(a) est du signe opposé à f(b) et si la fonction est continue et monotone (croissante ou bien décroissante) entre a et b alors le fonction s'annule une fois et une seule entre a et b

ici au départ on f(a) = f(0) > 0 et f(b) = f(1) < 0
cela ne figure pas explicitement dans l'algorithme mais dans la tête de celui qui l'a conçu quand il a choisi les valeurs initiales a = 0 et b = 1

on calcule le point milieu M au milieu de AB et on teste le signe de f(m)
la solution sera dans l'un ou l'autre des deux intervalles moitié selon le signe de f(m)

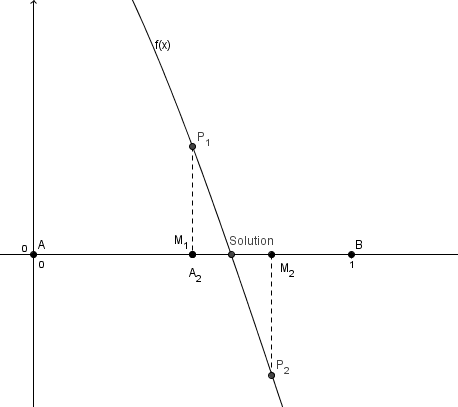
on recommence à partir de ce nouvel intervalle, ici en remplaçant a par m (m --> a)
et le nouveau milieu m2, puis en remplaçant ici b par m2 etc

comme à chaque fois l'intervalle est divisé par deux, on va encadrer la solution de façon de plus en plus précise, et on décide de s'arrêter lorsque cet intervalle est de longueur < la précision souhaitée.