Annuler
connectez vous
- Angles : angles adjacents, opposés, angles complémentaires, alternes, correspondantes... - Cours de cinquième
- Exercices sur les angles - cinquième
- Exercices sur les nombres en écriture fractionnaire - cinquième
- Dix problèmes pour revoir les acquis de la sixième - cinquième
- Vocabulaire cinquieme
- Seize Exercices portant sur le programme de cinquième
- Quatorze Exercices pour démarrer le calcul numérique - cinquième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. CinquièmeForum de cinquième Parallèles et anglesTopics traitant de parallèles et angles [tout]Lister tous les topics de mathématiques
Niveau cinquième
angle dans un quadrilatère
Posté par muriel 
bonjour 
,
bon je connais la solution, mais je vous soumets un exercice qu'un élève de 5ème m'a un jour posée:
comment peut-on démontrer que la somme des mesures des angles d'un quadrilatère est égale à 360°?
je rappelle qu'a ce niveau, le quadrilatère en question est convexe.
Bonsoir
Question subsidiaire : l'élève sait-il que que la somme des mesures des angles d'un triangle ... ?
Posté par nonoparadox (invité)re : angle dans un quadrilatère
Encore toi ! lol
Si tu poses en prérequis qu'on sait que la somme des angles d'un triangle est 180° , il suffit de couper ton quadrilatère en deux triangles, en traçant une des diagonales.
Maintenant pour démontrer que la somme des angles d'un triangle est égale à 180 ° , il suffit de mener par l'un des sommets du triangle la parallèle au côté opposé à ce sommet, et travailler avec des angles alternes-internes et correspondants. C'est difficile à expliquer sans dessin .... c'est comme ça que tu le résolvais ?
le problème dans votre idée, c'est que je ne vois pas le lien avec votre triangle, car vous couper vos angles en deux 
à oui, c'est bon j'ai compris 
bon et maintenant, s'il ne connais pas ce prérequis, comment faites vous?
Posté par nonoparadox (invité)re : angle dans un quadrilatère
Et sans redémontrer que la somme des angles d'un triangles est 180° ?
Posté par nonoparadox (invité)re : angle dans un quadrilatère
Ah oui t'as dit que tu t'en es pas servi ...
Posté par danskala (invité)re : angle dans un quadrilatère
Soit ABCD un quadrilatère et traçons sa diagonale [BD]
Dans le triangle ABD on a : .
Dans le triangle BDC on a : .
Donc
soit
Or
et
donc
Quels sont les prérequis ?
Angles alternes-internes ?
Angles à côtés parallèles ?
Symétrie centrale ?
....
Posté par danskala (invité)re : angle dans un quadrilatère
Et la somme des angles d'un pentagone (convexe) ?
Et la somme des angles d'un polygone à n côtés (convexe)?
les prérequis sont angles alternes internes, angles opposés par le sommet ...
conclusion: je viens de vous donner la solution
pour l'histoire des angles du polygone à n côtés, tout ce que je peux dire, c'est que cela doit tendre vers l'infini, non?
Posté par danskala (invité)re : angle dans un quadrilatère
Pour le pentagone c'est 540° je crois.
Et pour le polygone à n côtés je dirais 180
(n-2)°
Posté par danskala (invité)re : angle dans un quadrilatère
Je généralise ce que j'ai fait avec le quadrilatère.
Par exemple, dans mon pentagone je fais apparaître 3 triangles.
La somme des 3 angles du triangle ABC est égale à 180°.
La somme des 3 angles du triangle ACD est égale à 180°.
La somme des 3 angles du triangle ADE est égale à 180°.
La somme de ces 9 angles est égale à 1803 soit 540°.
Ensuite tu arranges ces 9 angles:
la somme des 2 bleus est égale à l'angle
la somme des 2 verts est égale à l'angle
la somme des 3 roses est égale à l'angle
Finalement tu arrives à la somme des 5 angles du pentagone qui vaut 540°.
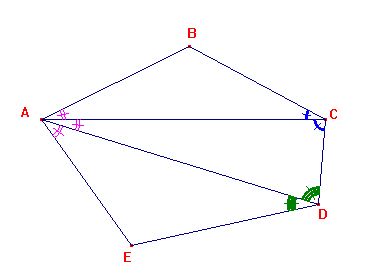
pour danskala
ok
pour rene38
voilà un dessin:
(ce qui est de la même couleur est soit parallèles: pour les droites; soit de même mesure: pour les angles)
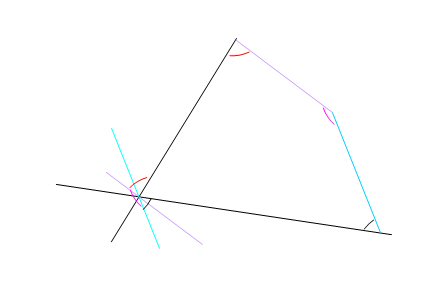
muriel > d'accord pour les 2 paires d'alternes-internes mais
- je ne vois pas d'utilisation d'angles opposés par le sommet
- comment justifies-tu la troisième égalité ?
j'avais mis trois petit point (ce qui voulait dire que j'ai mis en prérequis tout ce qui attrait au angle au niveau 5ème: alterne interne, correspondant, opposés par le sommet, complémentaire et supplémentaire)
donc il se peut que tu ne les utilises pas tous
ensuite, pour la 3ème égalité:
comment construis tu un angle?
n'oublies pas que les droites sont parallèles (donc même ouverture: définition de l'angle)
non?