Inscription / Connexion Nouveau Sujet
angles de tir maximal
Bonjour, je n'ai pas compris l'exercice si dessous :
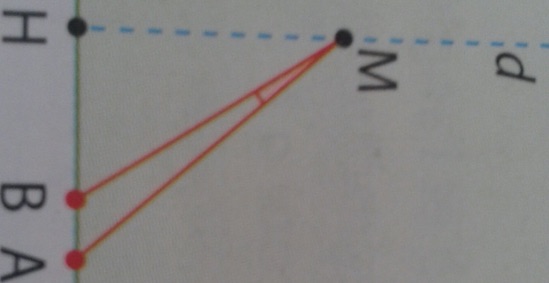
La figure ci-dessous représente un demi-terrain de rugby. A et B représentent les poteaux distants de 5,60 m. Un joueur a marqué un essai en H distant de 16,20 m de B. La règle veut qu'il place le ballon sur la droite d perpendiculaire à (AB) pour tirer son "coup de pied de transformation" qui doit passer entre les poteaux A et B.
Le but de l'exercice est de trouver la position du joueur représenté par le point M sur d pour que l'angle de tir angle AMB soit maximal.
On pose x=HM
1- En utilisant l'égalité angle AMH = angleAMH-angleBMH, montrer que cos angleAMH= (x^2+21,8*16,2)/racine de (21,8^2+x^2)(16,2^2+x^2)
2-Tracer à la calculatrice la courbe de la fonction de la variable x donnant la valeur en degré de l'angle AMB. Là est ce qu'il faut mettre l'égalité de la question 1?
3-Déterminer, à l'aide de la calculatrice, une valeur approchée de l'angle de tir maximal et la position du tireur.
Merci de bien vouloir m'aider.
Je n'ai pas réussie à mettre la figure. Mais est ce que tu peux m'aider sans la figure ou tu en as besoin obligatoirement.
vérifie les points (s'ils sont bien placés)
En utilisant l'égalité angle AMH = angleAMH-angleBMH
ne serait-ce pas : AMB=AMH-BMH ?
Si j'avais ta figure. Ce serait plus aisé.
La figure est dans l'autre sens. Oui j'ai fait une faute de frappe c'est bien AMB=AMH-BMH. Mon devoir est a rendre pour mardi prochain. Les points À et B se trouve en bas et le point H en fonction de B. Le point M est placé sur la perpendiculaire qui passe par H. Et le point M se balade sur la droite. Je ne peux pas mettre la figure car le fichier est trop lourd.
demande de précision : est écrit :
montrer que cos angleAMH= (x^2+21,8*16,2)/racine de (21,8^2+x^2)(16,2^2+x^2) : c'est bien retranscrit ?
cos(AMH)= HM/AM
AM²=x²+(16,20+5,60)²= x²+21,80²
AM=
(x²+21,80²)
cos(AMH)=x/
(x²+21,80²)bonjour,
je reprends tout
cos(HMB)= x/(x²+16,20²)
cos(HMA) =x/ (21,80²+x²)
cos(BMA)= cos(HMA-HMB)
appelons l'angle HMA=a et HMB=b
rappel: cos(a-b)= cosa*cosb + sina*sinb
cos(BMA)= x/(x²+16,20²)* x/ (21,80²+x²) + 16,20/(x²+16,20²) * 21,80/ (21,80²+x²)= (x²+21,8*16,2)/( (21,8^2+x^2)(16,2^2+x^2))
Annuler
connectez vous