Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Trigonométrie et fonctions trigonométriquesTopics traitant de trigonométrie et fonctions trigonométriques [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Angles orientés et parallélisme

Posté par
LanaS 02-02-13 à 15:19

Bonjour, j'ai un exercice à faire et je bloque, voici l'énoncé :

EX 1 :
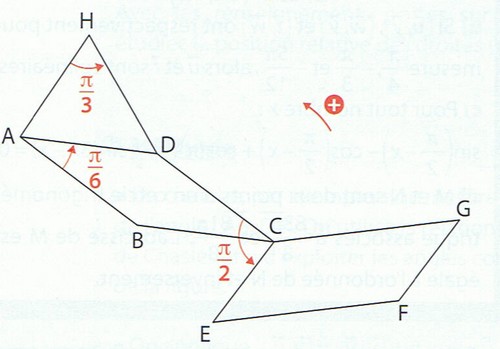
Dans le plan orienté, on considère la figure ci-dessous où ABCD et CEFG sont deux parallélogrammes tel que (\vec{AB} ;\vec{AD} ) = /6 et (\vec{CD} ;\vec{CE} ) = /2. ADH est un tirangle équilatéral tel que (\vec{HA} ;\vec{HD} ) = /3.
1. Décomposer l'angle de vecteur (\vec{AH} ;\vec{FG} ) en utilisant la relation de Chasles et les vecteurs AD et AB.
J'ai fais ceci : (\vec{AH} ;\vec{FG} ) = (\vec{AH} ;\vec{AB} ) + (\vec{AB} ;\vec{BC} ) + (\vec{CB} ;\vec{CE}) + (\vec{EF};\vec{FG}) mais je n'arrive pas à aller plus loin.

2. On veut démontrer que (\vec{AB};\vec{FG}) = /2
On ne trouve pas

Merci d'avance

Posté par
malou Webmasterre : Angles orientés et parallélisme 02-02-13 à 17:51

Bonjour

merci pour la figure

ensuite, il est écrit

Citation :
en utilisant la relation de Chasles et les vecteurs AD et AB.

c'est manifestement pas ce que tu fais

Citation :
On ne trouve pas

à tout ça, vous y arrivez pas;.;eh beh...

Posté par
LanaSre : Angles orientés et parallélisme 02-02-13 à 17:58

Autant pour moi voici la figure, oubli de ma part.
Je ne vois pas ce que AD peut faire dans cette décomposition

Angles orientés et parallélisme

Posté par
malou Webmasterre : Angles orientés et parallélisme 02-02-13 à 18:21

eh bien passe exactement par ce qui est dit dans l'énoncé...ça passe impeccable

essaie

Posté par
LanaSre : Angles orientés et parallélisme 02-02-13 à 19:05

Ça donne ça non ? : (\vec {AB};\vec {AD}) + (\vec {DC};\vec {CE}) + (\vec {EF};\vec {FG})

Posté par
LanaSre : Angles orientés et parallélisme 02-02-13 à 19:06

Désolé double post, j'ai oublié les balises LateX
\\ (\vec {AB};\vec {AD}) + (\vec {DC};\vec {CE}) + (\vec {EF};\vec {FG})

Posté par
malou Webmasterre : Angles orientés et parallélisme 02-02-13 à 19:40

tu dois commencer avec vecAH et finir avec vecFG
et utiliser ce que te dit ton énoncé

et aie un oeil sur la figure pour voir si tu seras capable de déterminer la valeur des angles

Posté par
LanaSre : Angles orientés et parallélisme 02-02-13 à 19:48

(\vec {AH};\vec {AB}) + (\vec {AB};\vec {AD}) + (\vec {DC};\vec {CE}) + (\vec {EF};\vec {FG})
Raah ça m'énerve je pense pas que ce soit ça.
Et puis si je passe par un autre chemin je n'aurai pas les angles

Posté par
malou Webmasterre : Angles orientés et parallélisme 02-02-13 à 20:12

on disait AD et AB
pourquoi ne pas les prendre dans cet ordre...

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 09:47

(\vec {AH};\vec {AD}) + (\vec {DC};\vec {CE}) + (\vec {EF};\vec {FG})?
Si je met AB je vais devoir revenir en arrière pour aller au même endroit, ça n'a pas de sens

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 09:52

Citation :
(\vec {AH};\vec {AD})+.....


bon début!...mais obéis, bon sang!.....si l'énoncé te dit ça, c'est que cela va fonctionner...

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 09:57

(\vec {AH};\vec {AD}) + (\vec {AD};\vec {AB}) + (\vec {BC};\vec {CE}) + (\vec {CE};\vec {EF}) + (\vec {EF};\vec {FG}) ?

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 10:03

(\vec {AH};\vec {AD}) + (\vec {AD};\vec {AB}) + ....

une fois à AB, faudrait peut-être le reprendre pour le suivant, non ?

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 10:05

(\vec {AH};\vec {AD}) + (\vec {AD};\vec {AB}) + (\vec {AB};\vec {BC})+(\vec {BC};\vec {CE}) + (\vec {CE};\vec {EF}) + (\vec {EF};\vec {FG})

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 10:07

(\vec {AH};\vec {AD}) + (\vec {AD};\vec {AB}) + (\vec {AB};\vec {FC})

tout simplement

heureusement que j'avais écrit hier :

Citation :
et aie un oeil sur la figure pour voir si tu seras capable de déterminer la valeur des angles

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 10:11

Mais je dois finir avec FG alors pourquoi il y a FC ?

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 10:13

erreur de frappe...c'est FG

(\vec {AH};\vec {AD}) + (\vec {AD};\vec {AB}) + (\vec {AB};\vec {FG})

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 10:15

Merci
Après j'ai décomposé (AB;FG) mais je passe par un chemin où je n'ai pas les angles...

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 10:18

mais tu ne dois pas le décomposer justement

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 12:28

Bah comment je fais pour trouver que (\vec {AB};\vec {FG}) soit égal à /2 vu qu'ils n'ont aucune lettre en commum

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 12:44

quand des vecteurs n'ont aucun point commun

tu prends un point O par exemple dans ton plan (ailleurs)
en O tu dessines le 1er vecteur AB
puis
toujours en O tu dessines le second vecteur FG
et tu lis ton angle facilement

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 13:14

Mais je n'ai pas de plan. Et je dois prouver que AH et FG sont parallèles

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 13:43

ta feuille de papier, c'est pas un plan....

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 13:44

ta figure
c'est bien de a géométrie plane...;donc tu es dans un plan!

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 13:46

Oui mais O comment je le place ? N'importe où ?
Et cette figure est ur mon livre je n'ai pas de mesure exacte

Posté par
malou Webmasterre : Angles orientés et parallélisme 03-02-13 à 13:51

Oui mais O comment je le place ? N'importe où ?

OUI!

Et cette figure est ur mon livre je n'ai pas de mesure exacte

mets ta feuille à côté

Posté par
LanaSre : Angles orientés et parallélisme 03-02-13 à 14:06

Je n'ai pas compris =/
Tant pis j'ai zappé cette question vu qu'on nous donne le résultat, j'ai fait la question d'après qui me demande de calculer l'angle (\vec {AH};\vec {FG}), je trouve \frac {6\pi}{6}, qui équivaut à , donc (AH) et (FG) sont parallèles

Merci pour votre aide =)


Rechercher
Menu
Espace membre
20 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !