pour les 2 premiere ...

1)  2x+1   --- coeff 2
2)   3x+1   --- coeff 3

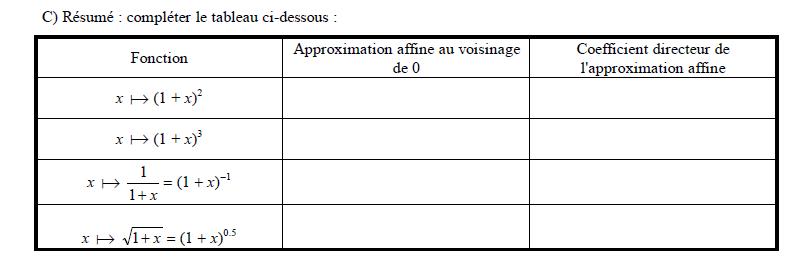
bonjour,

l'approximation affine sera pour chaque fonction x ---> f'(0).x + f(0)

pour la première ça donne: x---> 2x+2

je suis d'accord pour le 2x
Mais pour le 2 ?

f(0) = (1+0)² = 1

un point pour toi!

Mais je narrive pas le 3e et 4e ?
Pouvez vous mexpliquer ?

pour f'(x) , tu utilises la formule :

si f(x) = (ax+b)ⁿ alors f'(x) = n.(ax+b)^n-1.a


donc

et tu l'utilises dans ta formule.


idem pour le 4

à toi!

Mais dans le 3) f(x) c'est koi ?

1/1+x ou (1+x)^-1 ...???

????

f(x) = (x+1)^-1 pour que ce soit de la forme (ax+b)ⁿ avec a= 1 , b = 1 , n= -1

mais c koi alors 1/1+x ??

ah jai comrpis

oki !

(je pense que tu as vu que c'est la même fonction écrite différemment pour pouvoir utiliser cette formule de dérivation )

Poue le 3 )  -x+1 avec -1 coeff directeur
Pour la 4 ) 1/2 x +1 avec 1/2 coeff directeur

c'est juste !

Et avec ceci jdois faire un exemple
....

je narrive pas a simplifier , pouvez vous me mettre sur la voie svp ?

** image supprimée **
-------------------------
Je narrive pas a simplifier, pouvez vous  me mettre sur la voie

*** message déplacé ***

woooow... j'ai refait le calcul plusieurs fois , mais je cale...

j'ai remarqué que mais so far, ça n'aboutit pas...

je continue à chercher.

en faisant la difference tout s'annule sauf un fichu terme en 4x...

je recommence une derniere fois!

ah ben non c'est bon !

calcule la difference - ( le terme de droite) , mets au meme denominateur et tout se simplifie !
tu trouves 0 ce qui prouve l'egalité.

sous quel meme denominateur ?

re-

ça c'est du multipost anto2b...

*** message déplacé ***

anto2b; merci de consulter la FAQ du forum :
pièces jointes réservées aux images !, jamais de multi-post, etc...

cf. Etablir une egalité - racine cubique