Salut à tous,

Alors voilà, j'ai un problème sur l'approximation du nombre , qui me bloque complètement :


On inscrit dans un quart de disque de rayon 1, n rectangles de même largeur 1/n
.On conçoit qu'en augmentant le nombre n de rectangles, l'aire total de ces rectangles est de plus en plus proche de l'aire / 4 du quart de disque (partie A).
.On en déduit un algorithme pour obtenir une approximation du nombre pi (partie B).
(voire photo)

A. Expression de l'aire des rectangles

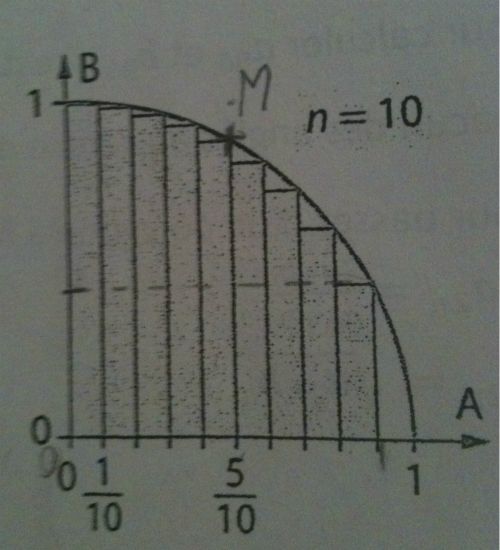
Sur le dessin ci contre, on a représenté dans un repère orthonormé, le quart de disque de rayon 1 dont les points ont des coordonnée (x ; y) positives.
On a partagé le rayon [OA] en 10 segments de même longueur, puis dessiné les rectangles comme indiqués sur la figure. On note S10 la somme des aires de ces rectangles.

On notera ainsi Sn(n>=2) la somme des aires des rectangles associés à un partage du rayon [OA] en n segment de même longueur.

1. Justifiez que l'équation
y=V(1-x²), avec x appartenant [0;1], caractérise l'appartenance d'un point M(x;y) à l'arc de cercle AB
2. Exprimez alors S10, puis Sn

B. Utilisation d'un algorithme
(voir photo posté)
Dans l'algorithme ci contre écrit AlgoBox :
-La ligne 7 correspond au choix du nombre n de segments de même longueur utilisés dans le partage du segment [OA];
- le calcul de Sn est effectué dans la boucle (ligne 9 à 12)

1.a) Que reconnaissez vous dans la ligne 18 ?
b) Qu'obtient-on à l'affichage ?

2.a) Utilisez Algobox (ou votre calculatrice) pour calculer Sn pour des valeurs de n de plus en plus grandes (jusqu'à 100 000).

b) Donnez la précision obtenue pour n=1000

c) Pour obtenir une approximation du nombre pi, Archimède (IIIe siècle avant J-C) a utilisé deux polygones réguliers de 96 côtés :l'un inscrit dans le cercle, l'autre circonscrit au cercle, ce qui lui a permis d'obtenir l'encadrement :
3 + 10/71 < pi < 3 + 1/7

Comparez votre résultat avec la précision obtenue par Archimède.


A.
1.
OM= V((xO - xM)² + (yO- yM)²)
OM= V((1- y)² + (x)²)
    V (x² + y²) =1
    V ((x² + y²))² =1²
    (x² + y²) = 1
     x² + y² - 1 =0
     x² - 1 = -y²
     y² = 1- x²
     |y| = V(1- x²)

2.
           10
S10 = 1/10 V(1- (1/10)^2)
           i=1

         n
Sn = E 1/n V(1- (1/n)^2)
         i=1

B.Utilisation d'un algorithme
1.
à)F1 (x) = V(1-x^2)
On reconnais l'équation de caractérisation de l'appartenance d'un point M à l'arc de cercle AB
b) Je ne comprend pas vraiment la question

2. a) J'ai programmer l'algorithme sur Algobox, par contre je n'ai pas réussi à ajouter les lignes 17 et 18: " fonction numérique utilisée..."

Alors j'ai trouvé pour :
n= 10.   Sn = 1,8
n= 100 .  Sn = 1,98
n= 1000. Sn= 1,998
n=10 000. Sn= 1,9998
n= 100 000. Sn= 1,99998

b) n= 1000. Sn= 1,998

c) Je pense avoir un problème avec mon algorithme car 1,98 reste assez éloigné de !

Merci d'avance