Inscription / Connexion Nouveau Sujet
Archimède et une valeur approchée de pi
j'ai un DM pour jeudi, j'arrive bien jusqu'à la question 3 car constructionn mais je ne sais pas comment répondre aux questions 4 et 5 . Pouvez vous m'aider, s'il vous plait.
On veut démontrer dans ce devoir que 3 < π < 2, pour cela, on va chercher longueur EB qui est un des 6 côtés de l'hexagone régulier inscrit dans le cercle. Puis la longueur BH qui est la moitié de la longueur d'un des 6 côtés de l'hexagone circonscrit au cercle.
1.Tracer une triangle ABC rectangle isocèle en A tel que AB = 1
(On prendra pour échelle : 1 unité = 5 cm).
2. Tracer le quart de cercle de centre A passant par C et B et placer E tel que ABE soit un triangle isocèle en E inscrit ce cercle.
3. Tracer le triangle ABH tel que (AH) soit la bissectrice de l'angle et Les droite (BH) et (AC) sont parallèles.
4. a) Montrer que l'angle
b) Montrer que le triangle ABE est isocèle en A
c) En déduire que ABE est équilatéral et que EB = 1.
d) En déduire le périmètre de l'hexagone inscrit dans le cercle.
5. a) Montrer que le triangle ABH est rectangle en H.
b) Calculer la valeur exacte de la longueur BH dans le triangle ABH.
c) En déduire le périmètre de l'hexagone circonscrit au cercle.
6. Quel est le périmètre du cercle
7. En déduire l'encadrement demandé.
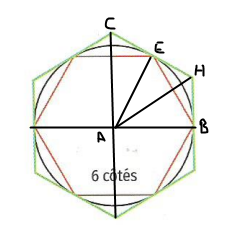
On veut démontrer dans ce devoir que 3 < π < 2racine3
4. a) Montrer que l'angle BAE = 60°
b) Montrer que le triangle ABE est isocèle en A
c) En déduire que ABE est équilatéral et que EB = 1.
d) En déduire le périmètre de l'hexagone inscrit dans le cercle.
5. a) Montrer que le triangle ABH est rectangle en B.
b) Calculer la valeur exacte de la longueur BH dans le triangle ABH.
c) En déduire le périmètre de l'hexagone circonscrit au cercle.
6. Quel est le périmètre du cercle
7. En déduire l'encadrement demandé.
L'hexagone régulier isométrique s'inscrit dans un cercle et la longueur de chacun de ses côtés est égal au rayon du cercle circonscrit.
Il est donc constitué de 6 triangles .......................
Je ne vois pas comment dire que l'angle est de 60° si on ne démontre pas qu'il est équilatéral or on nous pose la question en c et j'ai déduit q'uil était équilatéral avant la questions, il n"y a pas un autre moyen de trouver 60°
OK
Appliquons
Le Théorème de l'angle inscrit et de l'angle au centre
Considérons le point F point d'intersection du cercle et du diamètre passant par A et B
A toi
connait pas et je ne vois pas comment trouver le 60 ° sans démontrer que le triangle est équilatéral. ou sinon je répond à la question a après avoir répondu à b et c
L'angle au centre FAE. ntercepte l'arc .. De valeur........degrés
L'arc inscrit FBE (ABE) intercepte l'arc......
Le théorème de l'angle au centre affirme que, dans un cercle, un angle au centre mesure le double d'un angle inscrit interceptant le même arc.
L'angle au centre FAE. ntercepte l'arc FE. De valeur........degrés
L'arc inscrit FBE (ABE) intercepte l'arc FE
Considérons le point F point d'intersection du cercle et du diamètre passant par A et B
Trace la droite AB
Cette droite va couper le cercle en un point que l'on va appeler F
Ok
Vous croyez que je peux citer la propriété des points d'un cercle que je montre que AC=AE=AB donc le triangle ABE est isocèle en A .
on sait que ABE est isocèle en E et en A alors AE =EB et AE=AB donc AE=EB=AB, on en déduit que le triangle ABE est équilatéral et que AE=EB=AB=1.
Comme le triangle est équilatéral on a l'angle BAE = 180/3=60°
L'angle au centre FAE. ntercepte l'arc FE. De valeur 120 .degrés
L'arc inscrit FBE (ABE) intercepte l'arc FE
On sait que : Le théorème de l'angle au centre affirme que, dans un cercle, un angle au centre mesure le double d'un angle inscrit interceptant le même arc.
Donc L'arc inscrit FBE ( ou ABE) intercepte l'arc FE et vaut donc ........
Et c'est fini.
Tu trace la doite AB
Cette droite va couper le cercle en B et en F ( on aurait pu choisir une autre lettre) point opposé diamétralement à B
Tu as donc un diamètre [FB]
l'hexagone régulier inscrit dans le cercle.
Donc 6 côtés égaux ' 6 arcs egaus de 60 degrés.
L'arc FE vaut 2 fois 60.degrés donc 120 degrés
Relis l'énoncé
. < π < 2, pour cela, on va chercher longueur EB qui est un des 6 côtés de l'hexagone régulier inscrit dans le cercle.
pourquoi on doit faire le théorème et non dire,
EB est un des 6 côtés de l'hexagone régulier inscrit dans le cercle, on a pas conséquent 6 angles de centre A égaux 360/6=60° et donc BAE = 60°
Ce n'est pas très rigoureux.
L'angle au centre FAE. ntercepte l'arc FE. De valeur 120 .degrés
L'arc inscrit FBE (ABE) intercepte l'arc FE
On sait que : Le théorème de l'angle au centre affirme que, dans un cercle, un angle au centre mesure le double d'un angle inscrit interceptant le même arc.
Donc L'arc inscrit FBE ( ou ABE) intercepte l'arc FE et vaut donc 120/2 =60°
Ce théorème a été vu en troisième. Le covid l' avalé 
c'est bizarre même en confinement on ne m'en a jamais parlé. et pour les autres réponses en déduire le périmètre de l'exagone
ou plus simple (sans le théorème de l'angle au centre), on sait que BAE est isocèle (puisque AB = AE) et BAE = 60°
donc la somme des deux autres angles vaut 160-60 = 120 ° et comme ils sont égaux ils font donc 60° aussi. BAE qui a 3 angles égaux est donc équilatéral.
BAE = 60° c'est immédiat, l'hexagone a 6 cotés et des angles égaux, le total fait 2 radians donc un angle fait
radians donc un angle fait
2 /6 =
/6 =  /3 radians = 60 °
/3 radians = 60 °
vous croyez que je peux marquer pour la question
4.
a)
On sait d'après l'énoncé que EB est un des 6 côtés de l'hexagone régulier inscrit dans le cercle
Pour un hexagone régulier, les angles au centre interceptant les côtés de l'hexagone mesurent : 360 ÷ 6 = 60°.
BAE est un angle au centre A du cercle et interceptant le côté EB de l'hexagone inscrit dans le cercle donc BAE = 60°
On sait d'après l'énoncé que EB est un des 6 côtés de l'hexagone régulier inscrit dans le cercle
Pour un hexagone régulier, les angles au centre interceptant les côtés de l'hexagone mesurent : 360 ÷ 6 = 60°.
oui tu peux.
et pour montrer que le triangle ABH est rectangle en B?
Par construction BH est tangente au cercle donc perpendiculaire à AB qui est un rayon.


