Inscription / Connexion Nouveau Sujet
Associer une courbe a une fonction
Bonjour 
Voilà, je commence tout juste un exercice où on a 2 courbes et dans l'annoncé on nous dit "Les deux courbes C1 et C2, tracées sur [0;+  [ représentent les fonctions h et H telles que H'=h "
[ représentent les fonctions h et H telles que H'=h "
On doit alors associer chaque courbe a sa fonction, mais je ne vois pas comment avec ces seules informations là, y arriver. Merci d'avance pour votre aide. 
Bonjour,
Tu as très certainement une des 2 courbes qui descend vers un point, puis remonte, ou l'inverse.
Non ?
Alors tu remarqueras que ta deuxième courbe coupe l'axe des x au même endroit (pour la même valeur de x) que la 1ere courbe s'infléchit.
N'est-ce pas ?
Ah non, je n'ai pas ça du tout :/ Est-ce que je peux poster une photo sur ce forum ? (je suis nouvelle ici)
Oui, tu peux, en clickant sur image en dessous.
Par contre, il ne faut pas qu'elle soit trop lourde.
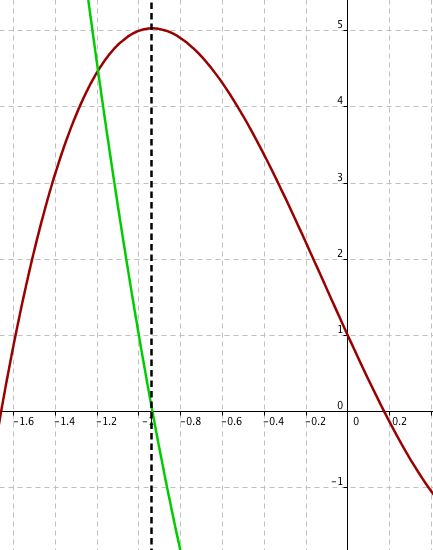
Tu vois,ta courbe en rouge plein a "une bosse" pile à l'endroit ou ta courbe en pointillée coupe l'axe des x.
C'est ce que je te disais . 

Tu remarqueras aussi que ta courbe en rouge plein a aussi "un creux" pile à l'endroit ou ta courbe en pointillée coupe l'axe des x.
Ah oui exact, je n'avais pas vu ça comme ça ! Donc j'imagine que H est la courbe en pointillée et h celle en continue ?
Car on voit que quand la courbe en continue admet un maxima ou un minima la courbe en pointillée coupe l'axe des abscisses au même point. (Oui je sais c'est très très mal formulé mais je ne vois pas comment l'expliquer d'une autre manière)
2 questions :
1 : qu'est-ce qui te fait dire cela ?
2 : entre H' et h, quelle est la dérivée de l'autre ?
1) Car la courbe coupe en pointillée l'axe des abscisses quand la courbe continue admet un maxima ou un minima
2) H' est la dérivée de h
1) Car la courbe coupe en pointillée l'axe des abscisses quand la courbe continue admet un maxima ou un minima
Et qu'est-ce que ça veut dire au juste cela ? Comment interprètes-tu cela ?
2) H' est la dérivée de h
Non, h est égal à H' (h=H'), H' est donc la dérivée de H, h est donc la dérivée de H.
1) Mais à part ce que je viens de dire je ne sais comment interpréter cela :/
2) Ah oui, c'est vrai !!
Quand tu as une fonction f.
Puis sa dérivée f'.
Qu'est-ce que représente pour la courbe de f, le nombre f'(x) ?
Soit qu'elle est croissante, soit décroissante. Je ne vois pas à quelle conclusion vous voulez m'amener :/
f'(x) est le nombre dérivé de la fonction f en x.
Il correspond au coefficient directeur de la tangent à la courbe en ce point x.
De ce fait, si f'(x)>0, f est croissante (en ce point)
Si f'(x)<0, f est décroissante en ce point.
Si f'(x)=0 (donc que la courbe de la fonction dérivée de f s'annule (donc coupe l'axe des x) , la tangente à la courbe est donc parallèle à l'axe des x.
Comprends-tu cela ?
Si tu veux aller plus loin dans l'analyse, tu remarqueras aussi que ta courbe H admet un point d'inflexion.