Inscription / Connexion Nouveau Sujet
asymptotes et fonction log
Bonjour à tous
Dans un devoir sur une fonction je dois déterminer toutes les asymptotes. Voila la fonction
f(x) = x + ln (x²-1)
j'ai trouvé x=-1 et x=1 Quand x tend vers + ou - l'infini j'ai trouvé f(x)/x =1 mais quand je cherche le b de y=ax+b je trouve l'infini. Je trouve ça bizare car on dirait que la droite asymptotique à l'air d'exister.
Quelqu'un peut-il m'aider Merci d'avance
bonjour
f(x) = x + ln(x²-1) = x + ln(x²(1-1/x²) = x + lnx² + ln(1-1/x²) = x + 2ln|x| + ln(1-1/x²)
l'asymptote est donc une courbe g(x) = x + 2ln|x|, pas une droite
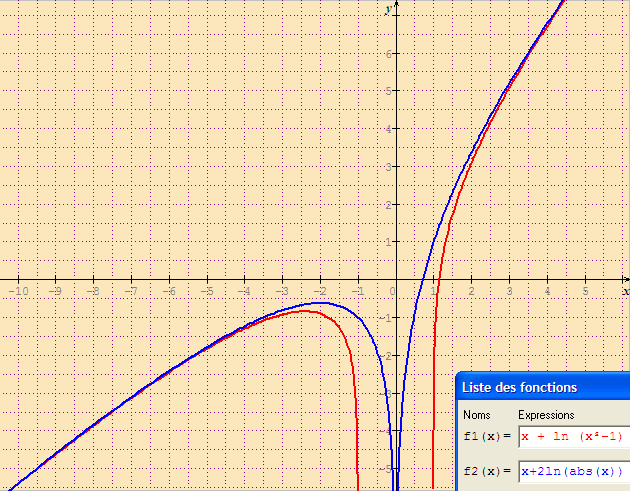
sauf erreur
Bonsoir merci pour la réponse
je pensais que les asymptotes étaient essentiellement des droites ou quelques fois des paraboles. Je n'ai jamais vu des asymptotes avec des log. C'est pas vraiment une asymptote ???
Une asymptote est une courbe vers laquelle tend la courbe que tu étudies
Pour des courbes en polaires, il peut y avoir des cercles asymptotes ...
--------------
par exemple
y = f(x) = x² + 1/x
a pour asymptote la parabole y=x² pour |x|->oo et l'hyperbole y=1/x pour |x|->0
comme le montre ce graphe :
d'autres auront peut-être d'autres avis...
Annuler
connectez vous