Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale DérivéesTopics traitant de Dérivées [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Bijection réciproque.

Posté par
matheux14 24-01-21 à 19:43

Bonsoir ,

Merci d'avance.

f est la fonction définie sur [0 ;1] par : f(x)=x-2\sqrt{x}+1.

On note (C) sa courbe représentative dans le plan muni d'un repère orthonormé (O ; I ; J).

1) Étudier la dérivabilité de f en 0. Interpréter graphiquement le résultat.

2) Démontrer que f est une bijection de [0 ;1 ] sur [0 ;1].

3-a) Démontrer que \forall x \in [0 ;1] , f \circ f(x)=x.

4) Construire (C).

Réponses

1) \forall x \in [0 ;1] , f(x)=x-2\sqrt{x}+1.

* f(0)=1

* \forall x \in [0 ;1] , \dfrac{f(x)-f(0)}{x-1}=\dfrac{x-2\sqrt{x}}{x-1}

D'où \lim_{x\to0}\dfrac{f(x)-f(0)}{x-1}=\lim_{x\to0}\dfrac{x-2\sqrt{x}}{x-1}=0

Donc f'd(0)=0 , f est donc dérivable en 0.

Par conséquent (C) admet au point d'abscisse 0 , une demi tangente de coefficient directeur 0.

2) * f est dérivable sur ]0 ;1[ , f'(x)=1-\dfrac{1}{4\sqrt{x}}=\dfrac{4\sqrt{x}-1}{4\sqrt{x}}

. 4\sqrt{x}-1=0 \iff x=\dfrac{1}{16}

. 4\sqrt{x}=0 \iff x=0

. Tableau de signe de f'(x).


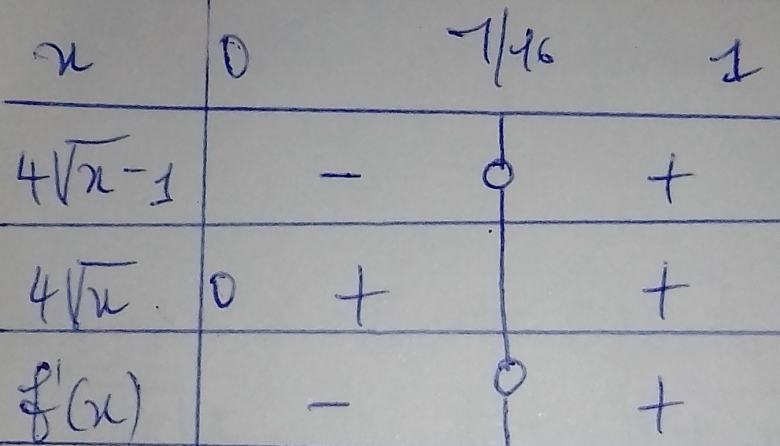
Bijection réciproque.

Pour le tableau de variation de f , f(x)=0 ==> x =1.

f(1/16)=9/16.

f décroît sur [0 ; 1/6]

Mais f(1)=0 or f'(x) > 0 sur ]1/16 ;1] donc f quitte 9/16 pour croître vers 0.. ce qui est impossible.

Mais je ne vois pas l'erreur que j'ai commis.

Posté par
phyelec78re : Bijection réciproque. 24-01-21 à 19:53

Bonjour,

Question 1)

tu appliques mal la formule de la dérivée, la dérivée en x0 de f (x) est :

f'(x_0)=  \lim_{x \to +x_0} \dfrac {f(x)-f(x_0)}{x-x_0}

ici x0=0 , alors pourquoi as-tu x-1 au dénominateur?

Posté par
carpediemre : Bijection réciproque. 24-01-21 à 19:53

salut

la nullité de la dérivée ne donne pas son signe !!

savoir pour quel x f'(x) = 0 ne dit pas pour quels x f'(x) > 0 ou f'(x) < 0 ...

il faut donc résoudre l'inéquation f'(x) \ge 0 (puisqu'un nombre n'a que deux signes) ...

et la question 2/ montre évidemment que tu t'es trompé ... (revois le coefficient 4)


il eut été plus judicieux de remarquer que f(x) = (\sqrt x - 1)^2

donc f'(x) = 2(\sqrt x - 1) \dfrac 1 {2 \sqrt x} dont le suigne est évident sur [0, 1]

Posté par
phyelec78re : Bijection réciproque. 24-01-21 à 19:58

Question 2) il y une erreur de calcul dans la dérivée :de sqrt{x}

Posté par
matheux14re : Bijection réciproque. 24-01-21 à 20:06

Ah oui

Merci

Posté par
matheux14re : Bijection réciproque. 24-01-21 à 21:17

Y a quelque chose qui cloche quand même..

Pour tout x de ]0 ;1[ , f'(x) >0

Par conséquent f est strictement croissante sur ]0 ;1[

Du coup f est continue et strictement croissante sur ]0 ;1[.

Donc f admet une bijection de [0 ;1] sur f([0 ;1])=[f(0) ;f(1)]= [1 ; 0]

Posté par
azerti75re : Bijection réciproque. 24-01-21 à 21:57

Bonsoir,

En attendant que carpediem ou phyelec78 reviennent:

matheux14 @ 24-01-2021 à 21:17

Y a quelque chose qui cloche quand même..

Pour tout x de ]0 ;1[ , f'(x) >0



Faux, recalcule la dérivée comme on te l'a demandé plus haut

Posté par
matheux14re : Bijection réciproque. 24-01-21 à 22:22

f'(x) = 2(\sqrt x - 1) \dfrac 1 {2 \sqrt x}=-\dfrac{\sqrt{x}-x}{x}

J'avais oublié le -

Donc pour tout x de [0 ; 1] , f'(x) ≤ 0.

Je crois que ça marche maintenant..

Posté par
phyelec78re : Bijection réciproque. 25-01-21 à 00:19


vous écrivez " Donc pour tout x de [0 ; 1] , f'(x) ≤ 0".  attention f'(x) non définie pour 0 donc crochet ouvert ]0,1]

Sinon,je ne comprends pas d'où vient ce signe "-",il y a un souci dans ton développement( si mon calcul est bon) voici :

f'(x)=2(\sqrt{x} -1)\dfrac1{2\sqrt{x}}=\dfrac{2\sqrt{x}}{2\sqrt{x}}-\dfrac{2}{2\sqrt{x}}=1-\dfrac1{\sqrt{x}}=\dfrac{\sqrt{x} -1}{\sqrt{x}}

Posté par
phyelec78re : Bijection réciproque. 25-01-21 à 00:24

Oups : erreur de ma part ton calcul est bon, tu as multiplié en haut et en bas par \sqrt{x}, je ne l'ai pas tout de suite remarqué. Sorry.

Posté par
matheux14re : Bijection réciproque. 25-01-21 à 07:54

Ok

3-a) Après avoir démontré que f o f(x)=x

3-b) Je dois en déduire la bijection réciproque de f.

Je fais comment ?

Posté par
alwafire : Bijection réciproque. 25-01-21 à 08:32

Bonjour

Utilise le fait que:pour   tout  x  de  [0;1]   fof^-1(x)=fof(x)=x  et  f  injective

Posté par
carpediemre : Bijection réciproque. 25-01-21 à 08:44

je ne comprends pas l'intérêt de développer mon expression : on simplifie par deux num et dénom et puis c'est tout !!!

f'(x) = 2(\sqrt x - 1) \dfrac 1 {2 \sqrt x} (\sqrt x - 1) \dfrac 1 {\sqrt x}

le quotient est trivialement positif par définition de la racine carrée

donc f'(x) a même signe que \sqrt x - 1 .... qui est évident sur l'intervalle ]0, 1]


le calcul de f o f montrer alors immédiatement que f est sa propre réciproque ...

Posté par
Sylvieg Moderateurre : Bijection réciproque. 25-01-21 à 08:54

Bonjour,
Je rajoute un " = " passé à la trappe

f'(x) = 2(\sqrt x - 1) \dfrac 1 {2 \sqrt x} = (\sqrt x - 1) \dfrac 1 {\sqrt x}

Posté par
matheux14re : Bijection réciproque. 26-01-21 à 14:23

alwafi @ 25-01-2021 à 08:32

Bonjour

Utilise le fait que:pour   tout  x  de  [0;1]   fof^{-1}(x)=fof(x)=x  et  f  injective


Pourquoi pour   tout  x  de  [0;1]   fof^{-1}(x)=fof(x)=x ?

Quel intérêt ?

Posté par
carpediemre : Bijection réciproque. 26-01-21 à 14:29

si f est une bijection de I dans J alors sa bijection réciproque est l'unique fonction g de J dans I telle que f o g (x) = x  (qui est équivalent à g o f (x) = x)

ici f est bijective et f o f (x) = x donc donc la réciproque de f est ...

Posté par
alwafire : Bijection réciproque. 26-01-21 à 21:02

Bonsoir

Tu as montré que f est une bijection de [0;1] dans [0;1] (question 2) ) , donc f admet une

bijection réciproque f^-1 de [0;1] dans [0;1]

Tu as montré que pour tout   x  de [0;1] fof(x)=x (question 3) a) )

On a : pour tout   x  de [0;1]  fof^-{1}(x)=x  (propriété de ton cours)

Donc pour tout   x  de [0;1] f(f^-1(x))=f(f(x)) ,par suite f^-1(x)=f(x)

car f est injective(une bijection étant à la fois injective et surjective)


Rechercher
Menu
Espace membre
6 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1734 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !