Voir la correction
- Sept Exercices assez simples sur les fonctions en terminale
- Dix Exercices sur des notions étudiées avec les fonctions - terminale
- Autour de la convexité d'une fonction
- Le raisonnement par récurrence : principe et exemples rédigés
- Fonction exponentielle - Fiche de Cours terminale
- Fiche sur les nombres complexes - terminale
- Limites de fonctions - Cours sur les limites
- Cours sur les suites en Terminale S
Fiche de mathématiques
Ile mathématiques > maths Tale > Dérivées
f(x) = 4x³ + 2x + 6 sur D =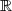
g(x) = e4x sur D =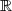
h(x) = 6x(2x² - 4) sur D =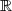
i(x) = (-5x³ + 4x)² sur D =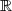
j(x) =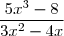
sur D =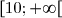 
P1(x) = 4x + 2
P2(x) = (3x + 5)(2x - 5)
P3(x) = x² + x - 6
P4(x) = x² + 2x + 1
f'(x) = 4 × 3 x² + 2 + 0 = 12x² + 2
g est de la forme eu.
On a : (eu)' = u'eu, donc :
g'(x) = 4 e4x
h est de la forme uv avec u = 6x et v = 2x² - 4.
On a : (uv)' = u'v + uv', donc :
h'(x) = 6(2x² - 4) + 6x × (2 × 2x) = 36x² - 24
i est de la forme un avec u = -5x3 + 4x et n = 2.
On a : (un)' = nun - 1u', donc :
i'(x) = 2(-5x³ + 4x)(-15x² + 4) = 150x5 - 160x³ + 32x
j est de la forme u/v avec u = 5x³ - 8 et v = 3x² - 4x.
On a :' = \dfrac{u'v - uv'}{v^2})
, donc :
 = \dfrac{5 \times 3x^2 \times (3x^2 - 4x) - (5x^3 - 8) \times (3 \times 2x - 4)}{(3x^2 - 4x)^2} = \dfrac{15x^4 - 40x^3 + 48x - 32}{(3x^2 - 4x)^2})
P1(x) = 0
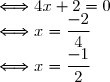
P2(x) = 0
(2x - 5) = 0\\ \Longleftrightarrow (3x + 5 ) = 0 \text{ ou } (2x - 5) = 0\\ \Longleftrightarrow x = -\dfrac{5}{3} \text{ ou } x = \dfrac{5}{2})
P3(x) = 0
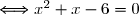
Calculons le discriminant :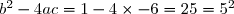
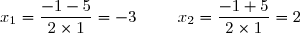
Donc : = 0 \Longleftrightarrow x = -3 \text{ ou } x = 2)
P4(x) = 0
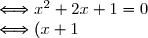^2 = 0\\ \Longleftrightarrow x = -1)
Publié par Tom_Pascal
le
Fonctions : Evaluation
exercice 1
Dériver les fonctions suivantes :f(x) = 4x³ + 2x + 6 sur D =
g(x) = e4x sur D =
h(x) = 6x(2x² - 4) sur D =
i(x) = (-5x³ + 4x)² sur D =
j(x) =
exercice 2
Trouver la ou les racine(s) des polynômes suivants :P1(x) = 4x + 2
P2(x) = (3x + 5)(2x - 5)
P3(x) = x² + x - 6
P4(x) = x² + 2x + 1
exercice 1
On sait que (xn)' = nxn - 1, donc :f'(x) = 4 × 3 x² + 2 + 0 = 12x² + 2
g est de la forme eu.
On a : (eu)' = u'eu, donc :
g'(x) = 4 e4x
h est de la forme uv avec u = 6x et v = 2x² - 4.
On a : (uv)' = u'v + uv', donc :
h'(x) = 6(2x² - 4) + 6x × (2 × 2x) = 36x² - 24
i est de la forme un avec u = -5x3 + 4x et n = 2.
On a : (un)' = nun - 1u', donc :
i'(x) = 2(-5x³ + 4x)(-15x² + 4) = 150x5 - 160x³ + 32x
j est de la forme u/v avec u = 5x³ - 8 et v = 3x² - 4x.
On a :
exercice 2
Il faut dans ces exercices résoudre Pn(x) = 0 avec n entier compris entre 1 et 4.P1(x) = 0
P2(x) = 0
P3(x) = 0
Calculons le discriminant :
Donc :
P4(x) = 0
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter