Inscription / Connexion Nouveau Sujet
Calcul approché de pi grace a la méthode d'archimède
Bonjour à tous.
Voici l'énoncé de l'exercice qui me pose problèmes :
On se propose de déterminer une valeur approché de en utilisant la méthode d'Archimède
Le périmètre d'un cercle est majoré par celui de tout polygone régulier circonscrit et minoré par tout polygone régulier inscrit .On considère un cercle de rayon 1 .Partant d'un triangle équilatéral , on double le nombre de côtés afin d'obtenir un hexagone régulier. On note pn , respectivement qn le demi périmètre du polygone inscrit ; respectivement circonscrit. On note Ak les sommets du polygone inscrit et Bk les sommets du polygone circonscrit . Avec les notations du problème on remarque que le polygone possède 3x2^n cotés .
(voir figure jointe)
1 ) Construire la figure pour le cas ou n = 1 ( c'est à dire dans le cas de l'hexagone ) . Quelle est la mesure de l'angle A(k)OA(k+1) ? et B(k)OA(k+1) ?
2 ) Calculer p1 et q1 .En déduire un premier encadrement de pi.
Cas général :
3 ) Exprimer en fonction de n . Dans la suite du problème on pose
(teta)n = et cn = cos (teta)n .
4 ) Calculer pn en fonction de n .
5 ) Montrer que pn = p(n+1)x c(n+1) .
6 ) Exprimer qn en fonction de pn et cn .
7 ) a )Montrer que c0 = 1/2 et c(n+1) = (racine carré)( (1+cn)/2 ) (1)
b ) Montrer par récurrence en utilisant (1) que pour tout entier naturel n
on a 0 < ou = cn < ou = 1 .
8 ) Montrer que les suites (pn ) et (qn ) sont deux suites adjacentes .
9 ) Montrer que la suite (pn ) converge vers pi .
10 ) Montrer que pour tout x positif on a , |sinx - x| < ou = (x^3)/(3!) et en déduire que pour tout entier naturel n une majoration de |pn-pi|.
11 ) Déterminer le plus petit entier naturel n pour obtenir une précision à 10-6 près de pi .
12 ) Accélération de la convergence .
On considère la suite définie par Un = (-pn + 4p(n+1)) / 3 pour tout entier naturel n ; montrer que cette suite converge vers .
Vérifier que la convergence est plus rapide que celle de la suite ( pn ) .
Alors en fait j'ai déja un problème avec l'énoncé ... Je suis en fait parti du principe que le polygone possèdant 3x2^n cotés était le polygone inscrit ; mais je ne suis pas vraiment sur que l'énoncé veuille dire ça ...
1) je trouve que l'angle A(k)OA(k+1) = 2pi/6 et B(k)OB(k+1)= 2pi/3
2) en suite je trouve p1 = 3 et q1 = 5.19 environ
3) je trouve A(k)OA(k+1)= 2pi/(3x2^n)
4) pn = 3 x ( 2-2cos(2pi/(3x2^n) ) mais le problème ici c'est que ca n'intègre pas cn ... étant donné que cn = cos (pi/3x2^n) ... A moins que je n'ai intégrer c(n-1) mais à ce moment là je n'arrive pas a trouver pour la question 5).
Donc je bloque à partir de cette question.
Si vous pouviez m'aider à me débloquer 
Merci beaucoup pour votre aide !
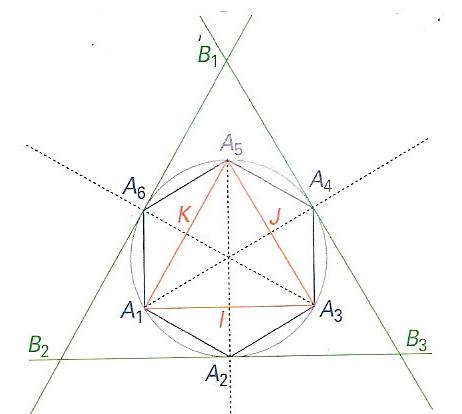
Ton problème est très mal posé, je comprends ton embarras. Il me semble qu'il s'agit ici de comparer les polynômes inscrits (rouge sur la figure jointe) et exinscrits (bleu). Dans le cas n=1, on a des hexagones. Le demi périmètre de l'hexagone inscrit est bien 3 comme tu l'as dit. Mais le demi-périmètre de l'hexagone exinscrit n'est pas 5.19 ! C'est plutôt 2 3 soit environ 3.46 !
3 soit environ 3.46 !
La formule que l'on te demande de trouver est
Pour n=1, on trouve
Pour n=2, on trouve
Pour n=10, on trouve
Ca, c'est pour savoir où tu vas...
Une fois que tu auras démontré la formule :
tu pourras dire que :
Alors,
Et, en vertu de la formule , on a donc :
Bonjour,
je ne comprend pas pourquoi:
A(k)OA(k+1)= pi/(3x2^n)
car pour n=1, A(k)OA(k+1)= pi/6
or A(k)OA(k+1)= pi/3 en réalité non? (j'ai fais 2pi/3x2^n)
Merci d'avance.


