Inscription / Connexion Nouveau Sujet
calcul d'aire
Bonjour,
je veux de l'aide pour cet exercice. Merci
Détermine l'aire du quadrilatère ayant pour sommet les points d'intersection de la circonférence d'équation avec les axes cartésiens
j'ai ceci :
cercle de centre I (3/2; 0) de rayon 5/2
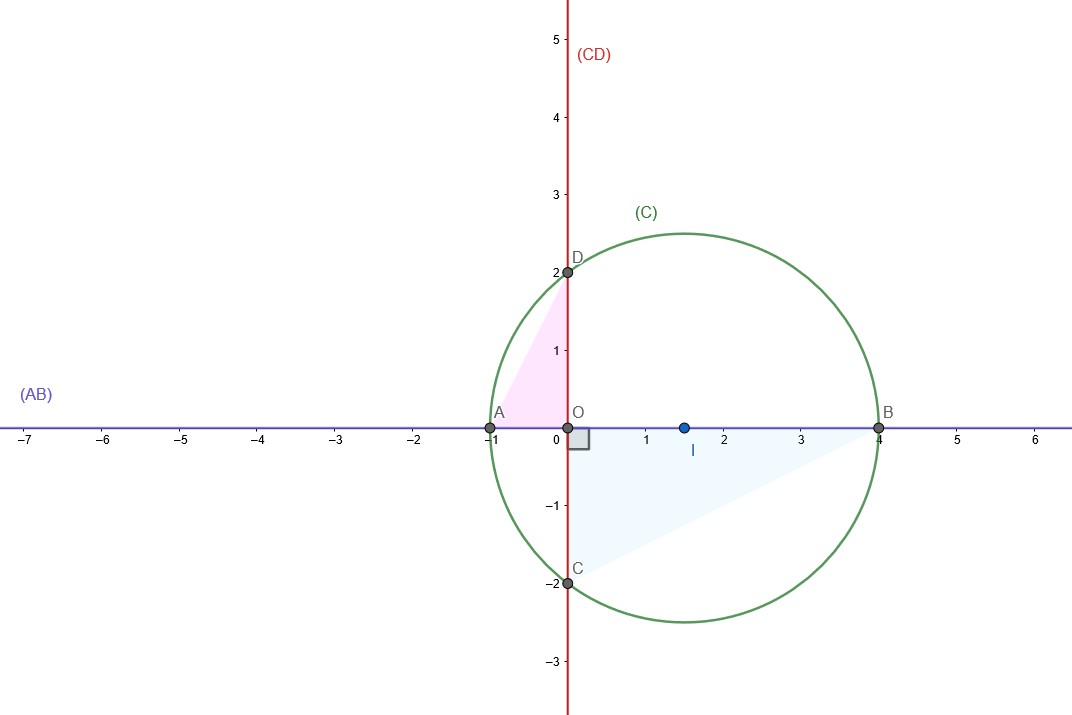
Points d'intersection A(0;0) ; B(3;0) ; C(0;-2) ; D(0;2)
Réduction de Gauss: donc OK pour le cercle.
Intersections avec l'axe Oy: on évalue en x = 0, ce qui donne et donc deux points
et
Intersections avec l'axe Ox: on évalue en y = 0, ce qui donne et donc deux points
et
. Donc pour le point B c'est (4,0), et non (2,0) ou (3,0)
Ensuite pour trouver l'aire, il ne suffit pas de faire un dessin et de compter les unités. En revanche, ça peut aider à voir que les droites (AB) et (CD) se coupent en (0,0) perpendiculairement, et donc, que
1) l'aire que tu cherches est découpable en 4 triangles rectangles
2) le travail est divisable par deux parce que le quadrilatère est symétrique par rapport à l'axe Ox
Donc deux calculs d'aire de triangles rectangles, tu sommes et tu multiplies le résultat par deux. On te regarde faire 
Bonsoir 
une petite précision :
Détermine l'aire du quadrilatère convexe ayant pour sommet les points d'intersection ...
On peut aussi remarquer que les deux triangles
et donc
sauf erreurLe déerminant est l'aire du parallélogramme de côtés AD et DB si je ne m'abuse alors qu elà on n'a pas deux côtés parallèles.
Il faudrait plutôt calculer .
Je sous-entendais plus haut que la hauteur de ABD est OD, donc que son aire est
Annuler
connectez vous
géométrie en post-bac