Bonjour,

J'aurais besoin d'un peu d'aide pour continuer mon exercice. Pouvez-vous m'aider s'il vous plait ?

Exercice (extrait) :
PARTIE A : Démontrer par récurrence que, pour tout entier naturel n strictement positif :
1²+2²+3²+…+n² = (n(n+1)(2n+1))/6 (j'ai réussi cette question)

PARTIE B : calcul d'une aire

f est la fonction définie sur [0 ;1] par f(x)=x².
Dans un repère, on note E la partie du plan délimitée par la courbe C représentant la fonction f, l'axe des abscisses et la droite d'équation x=1.
L'objet du problème est d'approcher et de calculer l'aire S de la partie E.
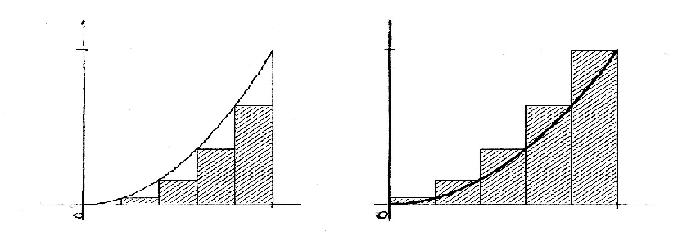
Pour cela, on divise l'intervalle [0 ;1] en n intervalles de même longueur (n entier naturel strictement positif) et on construit les rectangles comme il est indiqué sur les figures suivantes dans le cas où n=5.
(voir image ci-après)

On note Sn la somme des aires des rectangles contenus dans E et Tn la somme des aires des rectangles contenant E. On a donc pour tout n supérieur ou égale à 1, Sn < S < Tn

1) Calculer S5 et T5. On obtient en encadrement de S ; quel est son amplitude ? (j'ai trouvé : S5 = 0,24 et T5 = 0,44 ; encadrement : 0,24 < S < 0,44 ; amplitude = 0,2)

2) a) Vérifier l'égalité Sn = 1/n[(1/n)²+(2/n)²+…+((n-1)/n)²]
b) De même, vérifier l'égalité Tn = 1/n[(1/n)²+(2/n)²+…+(n/n)²]
c) Démontrer que Tn - Sn = 1/n

Je n'ai aucune idée pour ces trois questions

Merci d'avance