Niveau terminale

calcul d'une surface conique

Posté par
yoyore 06-12-09 à 16:36

Bonjour,
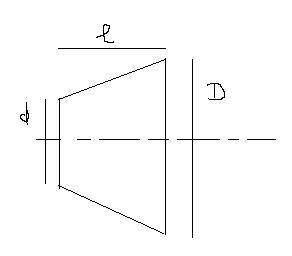
Je dois calculer une force exercée sur une surface conique.
Après avoir calculer la pression je peux donc en deduire la force
F = P x S
Mais je ne vois pas du tout comment calculer la surface.

Merci de votre aide

$calcul d\'une surface conique$

Posté par re : calcul d'une surface conique 07-12-09 à 14:27

Bonjour,

Un tronc de cône et son patron:

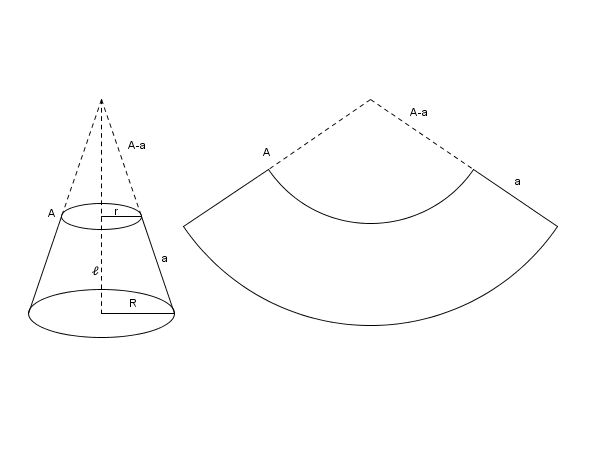
$calcul d\'une surface conique$

L' aire du cône complet: $\pi RA$

L' aire du petit cône: $\pi r(A-a)$

L' aire du tronc de cône par différence: $S=\pi RA-\pi r(A-a)=\pi a\left[\frac{A}{a}(R-r)+r\right]$

Or, $\frac{A}{R}=\frac{A-a}{r}=\frac{a}{R-r}$ (avec Thalès).

donc $\frac{A}{a}(R-r)=R$

et $S=\pi a(R+r)$

Avec tes notations: $a=\frac{r}{R}\ell=\frac{d}{D}\ell$

et $S=\frac{\pi}{2}\,\frac{d}{D}\,(D+d)\ell$

Posté par re : calcul d'une surface conique 07-12-09 à 14:36

Une erreur:

$a=\frac{R}{r}\ell=\frac{D}{d}\ell$

et $S=\frac{\pi}{2}\,\frac{D}{d}\,(D+d)\ell$

Posté par re : calcul d'une surface conique 07-12-09 à 16:58

Désolé, la fin est définitivement fausse...

A partir de $S=\pi a(R+r)$

On a avec Pythagore: $a^2=\ell^2+(R-r)^2=\ell^2+\frac{(D-d)^2}{4}$

Et $S=\frac{\pi}{4}(D+d)\sqrt{4\ell^2+(D-d)^2}$

Cette fois ci, je pense que c' est bon

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Fiches de niveau terminale
72 fiches de mathématiques en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

23 visiteurs

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

calcul d'une surface conique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths