Inscription / Connexion Nouveau Sujet
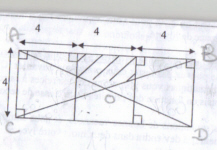
Calculer l'aire hachurée
Bonjour,
je ne sais pas comment calculer l'aire hachurée?
Faut-il que je calcule d'abord l'aire du triangle ABC et que j'enlève les 'petits triangles' par la suite?
Merci!
Salut 
Comment te dire... théorème de Thalès ça te dit quelque chose pour connaître la largeur du rectangle ?
Je voulais parler de la largeur du rectangle hachuré (du moins sur la figure on dirait que le polygone hachuré est un rectangle).
Bonjour Candice.
Le triangle AOB a la même base que le rectangle ABDC et la moitiè de sa hauteur. Son aire est donc le quart de celle du rectangle : 12*4 / 4 = 12.
Soient la base (horizontale) et la hauteur (verticale) du petit triangle rectangle dans la partie gauche du triangle AOB.
hauteur/BD = base/AB = 1/3.
La base du petit triangle est 4/3 et son aire (4 * 4/3)/2 = 8/3.
Le petit triangle rectangle dans la partie droite du triangle AOB est aussi égale à 8/3.
L'aire de la partie hachurée est 12 - 8/3 - 8/3.
Merci beaucoup plumemeteore!
Peux-tu juste m'expliquer pourquoi la base du petit triangle est 4/3, je n'ai pas compris?
salut,
la réponse de plumemeteore est la bonne.  quand au pourquoi du 4/3, utilise Thalès dans le triangles ABD et le "petit triangle" de sommet A, en haut à gauche.
quand au pourquoi du 4/3, utilise Thalès dans le triangles ABD et le "petit triangle" de sommet A, en haut à gauche. 
Dernière petit question (^^') Pourquoi l'aire du triangle AOB est le quart de celle du rectangle??
Merci et désolée de toutes mes questions ^^