Bonjour,

Je vais supposer que le carré CFED est de sens direct (c'est pas sûr si on regarde l'orientation de ton repère ...).

Dans ces conditions on a : .

On en déduit : et .

Voilà : il ne reste plus qu'à isoler les coordponnées de D et celles de E

Hum hum ... Dans mon cas, pour que l'application fonctionne dans tous les cas les coordonnées des points doivent être valable pour toute orientation du carré (cf remarque du 1er post).
Le carré est dans une base ou les vecteurs X et Y sont orthogonaux, il n'y a que 2 coordonnées x et y, si c'est ce que tu entends par "sens directe".

Alors si tu veux obtenir les coordonénes des points E et D, il y a 2 solutions ... Celle que j'ai donné correspond à un carré CFED de sens direct (c'est-à-dire qu'on énumère les sommets dans le sens trigonométrique conventionnel = sens giratoire du code de la route en France).

Oui le calcul est bon mais quand on calcul les coordonnées et que je traces le segment AB les point DF se trouvent en dessous de la ligne au lieu d'etre au dessus ...

Alors c'est que ton repère est de sens indirect ...

Bonsoir,

Arf j'ai essayé de remédier au problème de repère indirecte mais sans succès donc j'aurais aimé savoir comment on fait pour calculer les véritables coordonnées ??

:?

L'idée de base, très simple est de dire que si u(a,b) est un vecteur non nul dans le plan muni d'un repère orthonormé, alors il n'existe que 2 vecteurs qui sont à la fois de même norme que u et orthogonaux à u :

v(-b,a) et v'=-v(b,-a)

Pour choisir le vecteur qui convient, il faut définir une orientation du plan. Traditionnellement, le plan est orienté positif dans le sens giratoire du code de la route. Dans ce cas, c'est le vecteur v qui sera direct par rapport au vecteur u. C'est tout.

Peut-être pourrais-tu nous expliquer plus en détail ce que tu cherches...

Bonjour, c'est vrai j'aurai surement dut commencé par la...

En  fait les coordonnées que j'essaye de calculer rentre dans une programme qui a pour objectif de tracer une fractal, ici en l'occurrence c'est la forme quadratique de celle de Von Koch. Je construit cette  figure en appelant récursivement cette fonction sur chaque segment.
Mon dessin montre la première itération, puis après on rappel la fonction sur AC,CD,DE,EF et FB ...
Et le repère dans une fenêtre informatique est tel que l'axe des Y est orientè vers le bas et celui des x vers la droite. Le repère lui est fixe, mais par contre l'orientation des carrés évolue.

Voila j'espère que j'ai un plus éclairé le problème

En effet, tu aurais du commencer par là. Il se trouve que j'ai réfléchi, il y a très peu de temps, à propos d'une question posée sur ce même forum, sur la courbe de Von Koch. Voici mon bout de code (c'est du pascal mais tu devrais comprendre):

unit uVonKoch;

interface

uses
  Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
  StdCtrls;

type
  TForm1 = class(TForm)
    btNouveau: TButton;
    btPasAPas: TButton;
    procedure btNouveauClick(Sender: TObject);
    procedure btPasAPasClick(Sender: TObject);
    procedure FormActivate(Sender: TObject);
  private
    { Déclarations privées }
  public
    { Déclarations publiques }
  end;

var
  Form1: TForm1;
  Rayon,seuil : integer;
  xMax,yMax : integer;

implementation

{$R *.DFM}

Procedure VonKoch(xa,ya,xb,yb:real);
var xc,yc,xd,yd,xe,ye : real;
begin
   if sqr(xb-xa)+sqr(yb-ya)>Seuil then
   begin
      xc:=xa+(xb-xa)/3;
      yc:=ya+(yb-ya)/3;
      xe:=xa+2*(xb-xa)/3;
      ye:=ya+2*(yb-ya)/3;
      xd:=xc+0.5*(xe-xc)-sqrt(3)/2*(ye-yc);
      yd:=yc+0.5*(ye-yc)+sqrt(3)/2*(xe-xc);
      VonKoch(xa,ya,xc,yc);
      VonKoch(xc,yc,xd,yd);
      VonKoch(xd,yd,xe,ye);
      VonKoch(xe,ye,xb,yb);
   end
   else
   begin
      Form1.Canvas.MoveTo(round(xa),round(ya));
      Form1.Canvas.LineTo(round(xb),round(yb));
      form1.Canvas.Refresh;
      //sleep(1);
   end;
end;

procedure TForm1.FormActivate(Sender: TObject);
begin
   Seuil:=round(sqr(Form1.ClientHeight/3));
end;


procedure TForm1.btNouveauClick(Sender: TObject);
var xa,ya,xb,yb,xc,yc : real;      //sommets du triangle ABC
    ch : string;
begin
   XMax:=Form1.ClientWidth;
   Ymax:=Form1.ClientHeight;
   seuil:=40;
   with Form1.Canvas do
   begin
      Brush.Style:=bsSolid;
      Brush.Color:=clWhite;
      Rectangle(0,0,xMax,yMax);   //on dessine un rectangle blanc couvrant toute la surface
      Brush.Style:=bsClear;
      Pen.Color:=clBlue;
      //ch:=InputBox('Rayon du flocon (entre 80 et '+inttostr(YMax div 2)+')','Entrer le rayon','');
      ch:='200';
      rayon:=strtoint(ch);
      xa:=xMax/2+rayon*cos(5*pi/6);ya:=yMax/2+rayon*sin(5*pi/6);
      xb:=xMax/2+rayon*cos(pi/6);yb:=yMax/2+rayon*sin(pi/6);
      xc:=xMax/2;yc:=YMax div 2-rayon;
      VonKoch(xa,ya,xb,yb);
      VonKoch(xb,yb,xc,yc);
      VonKoch(xc,yc,xa,ya);
   end;
end;

procedure TForm1.btPasAPasClick(Sender: TObject);
var k : integer;
    xa,ya,xb,yb,xc,yc : real;
begin
   XMax:=Form1.ClientWidth;
   Ymax:=Form1.ClientHeight;
   rayon:=yMax div 2;
   xa:=xMax/2+rayon*cos(5*pi/6);ya:=yMax/2+rayon*sin(5*pi/6);
   xb:=xMax/2+rayon*cos(pi/6);yb:=yMax/2+rayon*sin(pi/6);
   xc:=xMax/2;yc:=YMax div 2-rayon;
   with Form1.Canvas do for k:=1 to 10 do
   begin
      Brush.Style:=bsSolid;
      Brush.Color:=clWhite;
      Rectangle(0,0,xMax,yMax);   //on dessine un rectangle blanc couvrant toute la surface
      Brush.Style:=bsClear;
      Pen.Color:=clBlue;
         VonKoch(xa,ya,xb,yb);
         VonKoch(xb,yb,xc,yc);
         VonKoch(xc,yc,xa,ya);
         Seuil:=Seuil div 3;
      pen.color:=clRed;
      Ellipse(xMax div 2-round(Rayon),yMax div 2-round(rayon),xMax div 2+round(rayon),yMax div 2+round(rayon));
      sleep(1000);
   end;
end;

end.

D'ailleurs, on regardant dans les anciens topics où j'ai participé, j'ai retrouvé la question concernant le flocon de Von Kioch et ... c'était déjà toi qui posait la question Algorithmique : flocon de Koch

Oui je sais c'est moi qui est posé cette question je te remercie une nouvelle fois pour ton aide qui fut très utile mon algo pour le flocon et le carré quadratique de Von Koch est à 2 ou 3 détails près identique mais il me reste que l'inconnu la détermination de la position des points D et E tou le reste est compris et assimilé

En fait pour bien recentrer mon problème, c'est la méthode que je n'arrive pas à comprendre pour calculer les points D et E pour cette fractal. Mais j'ai eu également le même problème pour la construction du flocon (cf image) pour le calcul du point D j'ai finalement trouvé les coordonnées de celui-ci en fonction des point C et E mais je n'ai pas trouvez la méthode ...

pour les coordonnées de D du flocon j'ai :

xD = (xC+xE)*cos 60°+(yE-yC)*sin 60°
yD = (yC+yE)*cos 60°-(xE-xC)*sin 60°

(avec ||AC|| = ||CD|| = ||DE|| = ||EB|| = ||AB||/3 )

et je voudrai faire la même méthode pour le carré si possible ou similaire pour trouver les coordonnées de E et D en utilisant peut être le triangle ACD pour D et EFB pour E.

Je ne comprends pas trop ta question.

Si je pars de ton schéma ci-dessus, en utilisant les nombres complexes, on peut dire que : avec .

À partir de là, on trouve facilement les coordonnées du point D non ?

Oui c'était bien là ma question ...j'ai fini par comprendre pourquoi ça n'allais pas je m'excuse de t'avoir déranger autant. Mon programme "ne fonctionnai pas" vraiment comme je voulais parce que le carré que je devais tracer devait être en bas et non en haut comme dans mon premier dessin. Donc avec les complexes j'ai fait une rotation de  = - /2 pour calculer les coordonnées de D et E ce qui m'a donné :

xD = xC + yF - yC
yD = yC - xF + xC

xE = xF + yB - yF
yE = yF - xB + xF

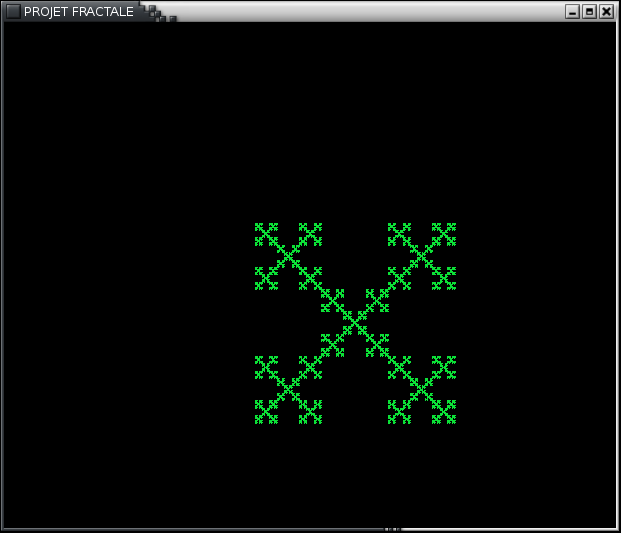
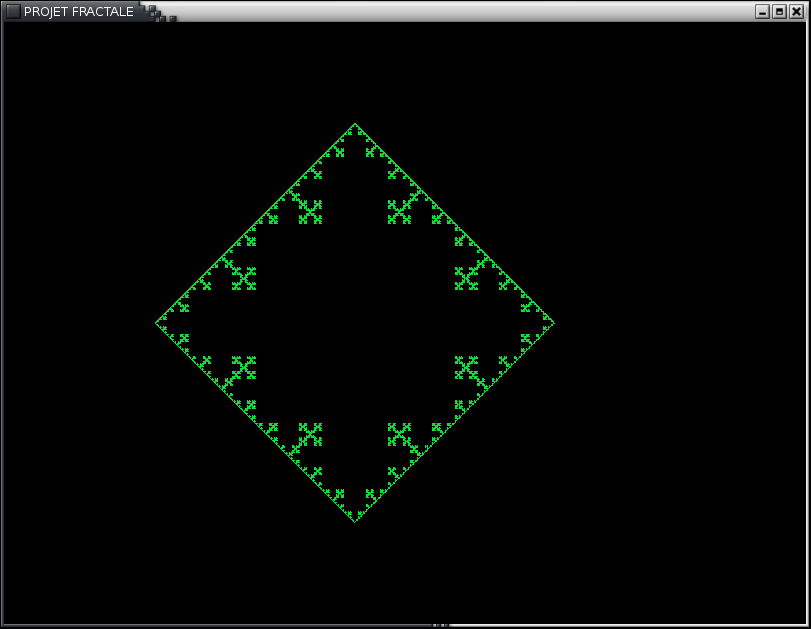
Qui donne  le carré de Von Koch(le carré)

et l'autre avec le carré au dessus qui donne le fractal Box (la croix)

Voila éh bien merci beaucoup pour ce laborieux coup de pouce

Heureux de t'avoir aidé