Inscription / Connexion Nouveau Sujet
Calculer une aire sous une courbe Intégrale
Voila j'ai un exercice en maths et j'suis vraiment perdu!
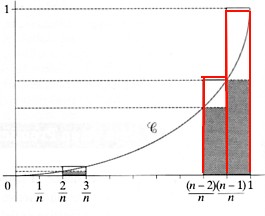
On considère la fonction carrée sur l'interaller [0;1] notée f et représentée par la courbe C.
On veut calculer l'aire sous la courbe C, c'est çà dire l'aire de la surface S comprise entre m'axe des abscisses, la courbe C et la droite d'équation x=1
On partage l'intervalle [0;1] en n intervalles de même longueur (1/n).
On construit alors sur ces intervalles n rectangles intérieurs à la surface S (en gris sur le dessin) et n rectangles qui contiennent S (aux contours rouges sur le dessin).
On note Un la somme des aires de la prmière famille de rectangles et Vn la sommes des aires de la deuxieme famille
1. Montrer que Un=1/(n3) [0²+1²+...+(n-1)²] = 1/(n3)  n-1 k=0 k²
n-1 k=0 k²
et Vn = 1/(n3) [1²+2²+ ...+n²] = 1/(n3)  n k=1 k²
n k=1 k²
2. Montrer par récurrence que  n k=1 k² = (n(n+1) (2n+1)) / 6
n k=1 k² = (n(n+1) (2n+1)) / 6
En déduire de nouvelles expressions des termes Un et Vn
3. Montrer que les deux suites sont adjacentes et calculer leur limite commune. En déduire une définition de l'aire de la surface S
4. Déterminer une fonction constante g définie sur l'intervalle [0;1] telle que l'aire sous sa courbe  soit égale à l'aire de la surface S
soit égale à l'aire de la surface S
Bonjour, exercice intéressant.
Je veux bien t'aider^^
Tu es d'accord que les rectangles on toujours même largeur ?
Ensuite pour avoir la hauteur, tu dois calculer f(...)=(...)²
Bien sur, les deux rectangles ont une hauteur différentes.
L'une est facile à trouver, pour l'autre il faut juste réfléchir un peu.
Déjà essaye de calculer U1,U2.. et V1, V2...
Puis tu pourras en déduire l'expression de Un.
Déjà remarque que tu as
Où un correspond à l'aire de n-ième rectangle.
si tu trouves un en fonction de n, tu trouves Un


