Je crois avoir trouvé:
On pose D=distance totale du domicile au stade.
d=distance parcourue jusqu'au point de rencontre des deux frères
t=temps écoulé depuis le démarrage du grand frère.

On a deux tableaux de proportionnalité:
pour le cadet:
[D ,1/2][d, t+5/60]
pour l'ainé
[D, 1/3][d,t]


il vient comme équations:
Dt=d/3
Dt+(5/60)D=d/2

soit
3Dt=2Dt+(5/30)D

on simplifie l'égalité par D:
3t=2t+5/30
t=5/30 heure
t=10 minutes

est-ce exact ?

Bonjour
euh...niveau 5e, profil licence maths


merci de préciser le contexte de la demande qu'on sache à quel niveau répondre

C'est pour un cours à un élève de 5ème. Le souci de ma démo est qu'il y a trop de paramètres pour un élève de 5ème.

oui, je suis d'accord avec toi
on ne peut pas expliquer ça comme ça à un élève de 5e
peut-être tout ramener à ce qui se passe en 1 minute

zut, je dois m'en aller

Bon, j'ai fait une démonstration mais celle-ci a un défaut rédhibitoire pour un niveau de 5ème, il y a trop d'inconnues et trop de paramètres.
Le challenge du fil est de trouver une démo accessible à un élève de 5ème, en supprimant le maximum d'inconnues.

Bonsoir,
Tout ramener à une minute permet effectivement de simplifier la résolution.

On peut partager le trajet en 60 parts égales.
Si D est la longueur du trajet, soit u = D/60.
Le jeune parcourt 2u en une minute.
Le grand parcourt 3u en une minute.
Quand le grand démarre, le jeune a déjà parcouru la distance 52u.
On cherche le nombre n de minutes pour que n3u = 10u + n2u.
On trouve n = 10.

Pas certaine que ça convienne pour une résolution en 5ème.

alors moi j'avais dit
en 1 minute, le grand parcourt 1/20 (de la distance)
le petit parcourt 1/30

le grand est parti 5 minutes après le petit qui a donc déjà parcouru 5/30 soit 1/6

en 1 minute toujours, la différence parcourue est 1/20 - 1/30 soit 1/60 et comme il doit rattraper 1/6,eh bien il va mettre 10 minutes

tout repose sur les fractions, aucune inconnue
pas facile quand même qu'un enfant de 5e trouve cela seul

Bonjour,
Il faut d'abord dire que ce problème n'est pas faisable.
L'auteur imagine sûrement que les vitesses sont constantes, mais alors il faut le dire  car cela n'arrive jamais dans la réalité.
Je suis d'accord avec Sylvieg, partager la distances en un nombre de parties égales est la bonne solution pour la classe de 5ème.
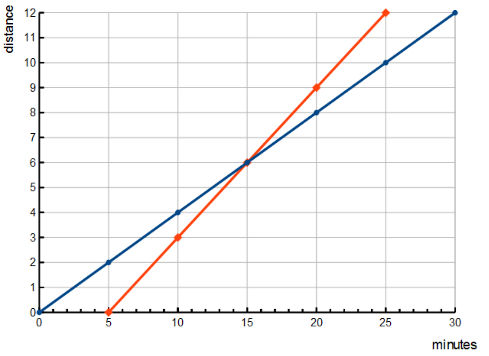
Moi j'ai choisi 12 unités et j'utilise le même raisonnement avec les distances parcourues en 5 minutes.
Mais on peut se passer des calculs en utilisant un graphique ( voir pièce jointe ).
La conclusion est que le grand frère n'est pas sympa. Quand il rejoint son petit frère il  le dépasse sans ralentir.
A moins qu'ils aient chacun leur voiture ?

LUCAS35, bonjour et bienvenue
puis-je te demander de renseigner ton niveau d'études s'il te plaît, nous le demandons à tous les nouveaux inscrits

extrait de la FAQ du forum :

Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau sujet ?

Oui, indiquer son niveau (dans son profil) et celui du problème est obligatoire lorsqu'on pose une question.

Un correcteur pourra ainsi facilement juger s'il est en mesure de vous aider ou non. En l'absence de cette précision, aussi bien sur votre profil que sur le forum dans lequel le sujet est publié, il risque moins de vous indiquer une méthode que vous n'avez pas encore vue en classe, etc.

De même, si vous êtes élèves dans un pays francophone, vous pouvez consulter les équivalences des systèmes de niveaux scolaires afin de choisir le niveau de la classe française correspondant à votre classe. Cela permet au correcteur d'intégrer le fait que votre niveau scolaire ne correspond pas forcément à celui stipulé dans les programmes français en vigueur.

Il est de même demandé aux aidants de renseigner leur profil, ce qui en général donne une bonne indication du niveau de l'aide apportée.