répondez-moi, pardon

Bonjour,

Suite géométrique... de premier terme 1 et de raison 0,9876 pour un siècle.

A l'instant de la mort la proportion de carbone 14 vaut 1 = 100 % de sa valeur pendant la vie
Puis cette proportion diminue
Après 100 ans il reste 100 % - 1,24 % = 98,76 % ou 0,9876 fois la valeur initiale
Après 200 ans il reste 0,9876 fois ce qu'il restait après 100 ans, c'est-à-dire qu'il reste 0,9876² fois la valeur initiale
etc.

Après 1 000 ans il reste 0,9876¹⁰ 0,8827 fois la valeur initiale

Etc.

ah ouai bien sûr, merci beaucoup, j'ai compris, si j'ai besoin d'aide pour les autres questions je te demanderai, merci

pardon pour les questions 3) et 4) comment fais-je?

pardon quelle est la valeur initiale?

excuse moi j'ai compris, il me manque seulement les questions 3) et 4)

s'il vous plait répondez moi le plus rapidement possible, je dois rendre ce dm le lundi 12 mai

je n'ai même pas su faire la 2)

Si tu as compris pour la première question, la deuxième n'est pas du tout différente.
Relis bien ma réponse du 09/05 à 07 h 53 : je t'ai sérieusement mis sur la piste de la réponse à la deuxième question.

Bonjour, moi je sollicite votre aide, pour juste la dernière question.
Certaine personne de ma classe m'on dit que c'était apparemment impossible avec notre niveau de 1 de faire la dernière question, ou du mois d'y répondre avec un raisonnement mathématiques, et que pour nous il fallait juste faire a la calculette et trouver la puissance jusqu'a ce soit égale a 0.1 de l'atmosphère initial.

Est ce vraie, ou on peut le faire ?

Merci de m'aider!

Bonjour,

C'est assez vrai.

La bonne manière est d'utiliser les logarithmes... mais tu ne l'as pas encore appris en 1^ère

Je vois deux manières de faire à ton niveau :
. aujourd'hui, en effet, on peut avec une calculatrice faire des essais et trouver ; cela peut d'ailleurs être fait avec méthode ; certains ordinateurs sont programmés ainsi pour des problèmes très compliqués que l'on ne sait pas résoudre autrement ;
. hier... sans calculatrice : tu fais un graphique et tu portes les différentes valeurs calculées aux questions précédentes : en abscisse le temps qui passe et en ordonnée le pourcentage de carbone 14 qui reste.
Ce graphique est ensuite lu dans l'autre sens : étant donné un pourcentage de carbone, tu peux lire à peu près l'âge. Cette méthode convient aussi très bien.

Ok, merci d'avoir repondu si rapidement, mais je pense pas que notre profs ai voulues que l'on fasse un graphique, on en a jamais fais pour les suites, et j'ai calculé, il faut allez jusqu'a U184 pour avoir 0.1 de l'initial.

Je pense que je marquerais la reponse au tac-o-tac et que j'ai utilisé la fonction tab de la calculatrice.

En tout cas merci beaucoup !!

Tu as bien fait :


Pour 10 % soit 0,1 de carbone 14 restant :
Soit n le nombre de siècles n = log(0,1)/log(0,9876) = 184,54

Donc... 18 454 ans (mais le résultat n'est pas aussi précis que cela)

Et pour 5 % soit 0,05 de carbone 14 restant ?

Utilise la touche log de ta calculette... tu auras appris quelque chose (même si tu comprends l'an prochain )

"Et pour 5 % soit 0,05 de carbone 14 restant ?

Utilise la touche log de ta calculette... tu auras appris quelque chose (même si tu comprends l'an prochain )"

J'ai cherche dans le menu de ma calculette j'ai pas de fonction log, et comme j'ai perdu la notice :/, j'ai regarde dans tab et recu aussi et je trouve pas log non plus.


En tout cas pour 5%, c'est 24 000 ans pile poil.

Merci pour votre aide encore !

Alors tu as peut-être une touche ln (comme logarithme népérien...)

Même possibilité n' = ln(0,05) / ln(0,9876) = 240

Donc 240 * 100 = 24 000 ans !

Je t'en prie et à une prochaine fois !

tu veux dire qu'il faut donc répondre en éssayant avec la calculatrice n'est-ce pas?

Comme je l'ai écrit le 11/05 à 18 h 53 :

Deux possibilités si tu n'utilises pas les logarithmes :
. par essais successifs à la calculatrice ;
. par lecture d'une courbe préalablement tracée.



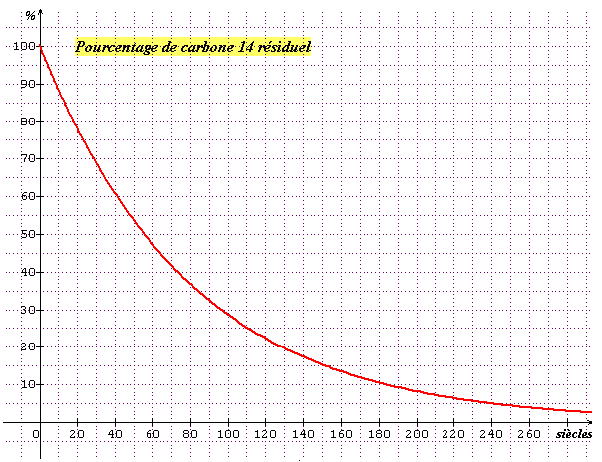
On retrouve bien sur cette courbe (merci Sinequanon) les valeurs cherchées : 184 siècles pour 10 % et 240 siècles pour 5 %

ok, merci beaucoup

je vous remercie vraiment de votre aide et de votre patience

Je t'en prie.
A une prochaine fois !