Inscription / Connexion Nouveau Sujet
Centre de l'homothétie
Bonjour
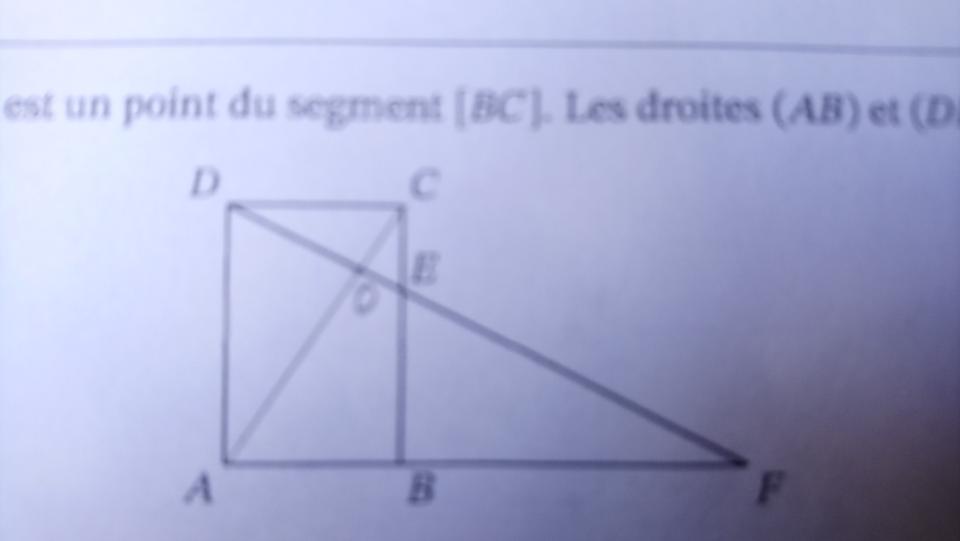
ABCD est un rectangle.
E est un point su segment [BC]
(AB) et (DE) se coupent en F
Justifier que les côtés de ADF sont parallèles aux côtés du triangle CDE.
Fait : j'ai utilisé les propriétés du rectangle
Placer O centre de l'homothétie qui transforme ADF en CDE.
J'ai tracé (AC)
Elle coupe (DF) en O
Est ce que c'est bien
A se transforme en C
D se transforme en E
Je ne comprends pas comment F se transforme en D
Merci
chaque sommet d'un des triangle doit se transformer en un sommet de l'autre donc si ADF se transforme en CED ça donne :
A se transforme en C
D se transforme en E
F se transforme en D
c'est pas choquant, on peut très bien avoir OA/OC = OD/OE = OF/OD
c'est pas parce que D se transforme en E que E doit se transformer en D, dans une homothétie OM' = kOM on a pas OM = kOM'