Inscription / Connexion Nouveau Sujet
cercle circonscrit
Bonjour,
Voila, je ne suis pas matheux pour deux sous mais je me rend compte que mes lacunes me porte préjudices...
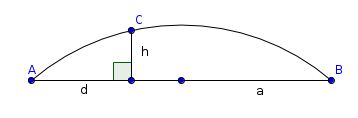
Comme mon pseudo l'indique , je suis menuisier et j'ai besoin de définir le rayon d'un cercle passant par trois points, ceci représentant le linteau d'une fenêtre ou d'une porte, cintré.
par des mesures, je définis mes trois points comme suit: largeur de l'ouverture puis la hauteur de la flèche entre ces deux points.
Me voila avec un triangle, souvent isocèle, ma largeur étant la base et la hauteur , ma flèche.
Donc ma question est, (par un calcul pouvant être repris dans un tableur):
comment définir le rayon du cercle passant par ces trois points?
Voila j'espère avoir été assez clair....
merci de votre aide.... au secours!!
Bonjour !
Si ton triangle est isocèle, de base (
est donc la moitié de ta largeur) et de hauteur
, le rayon
que tu cherches est
A ta disposition si tu as besoin d'autres explications.
Bonjour,
super, enfin des maths appliquées. ..
si tu appelles d la largeur de l'ouverture et h la hauteur de la flèche, tu as deux triangles rectangles de mêmes dimensions:R le rayon recherché pour l'hypothenuse, d/2 et r-h pour les autres côtés.
Pythagore nous dit:
r2=(d/2)2+(r-h)2
On en deduit: r=d2/(8rh) - h/2
Ça te va?
Et si ( désignant toujours la demi-largeur) on souhaite la hauteur
à l'aplomb d'un point à distance
d'une extrémité de la base :
Pour , on retrouve bien la formule précédente.
Pour lamenuis qu'est pas matheux, la solution de luzac est la plus simple.
Il faut quand même prendre garde au fait qu'on utilise là, la demi-largeur de l'ouverture...
En effet.
Mais entre toi qui ne répond pas à la question posée (je n'ai d'ailleurs pas compris ce dont tu parlais...) et moi qui y réponds mal,je me suis dit que lamenuis, menuisier et pas matheux, méritait qu'on lui précise la bonne réponse au milieu des délires! 
Non?
qui ne répond pas à la question posée
Lis mieux le message de départ :
Me voila avec un triangle, souvent isocèle, ma largeur étant la base et la hauteur , ma flèche.
Il ne t'aura pas échappé que "souvent" est différent de "toujours".
si si.. j'étais en train d'essayer de comprendre les réponses et de l'appliquer avec des dimensions.....
ta solution est impeccable....
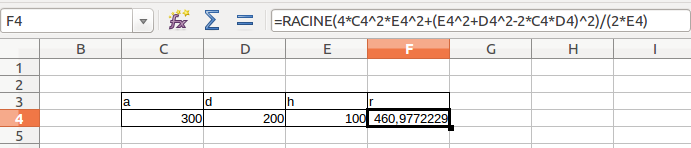
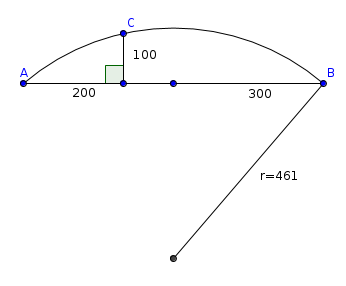
avec d= 1200 mm et h= 250mm
r= 1200²/(8*250)+250/2
ca me donne 845 après vérif au compas, ca colle, merci encore....
Si lamenuis est content, tout va bien. L'essentiel est préservé.
Robot, je te présente toutes mes excuses, mais quand tu écris
on souhaite la hauteur h à l'aplomb d'un point à distance d
Je m'attends, à la ligne suivante, à lire quelque chose qui commence pas "h=".
Donc, je suis très probablement un peu (tres) con, mais je ne comprends rien à ta proposition.
voilà, voilà, voilà.
he oui,robot merci quand meme.... mais j'ai décroché à... r=..... rires!!!
bon maintenant , faut que j'arrive a comprendre quand meme.....
par contre , c'est pas evident d'inserer une fraction dans une cellule d'un tableur?
du coup j'arrive pas trop a retranscrire avec mes dimensions....
Dans la cellule, Avec la formule de luzac, si a est en A1 et h en A2, tu peux mettre en A3: =(A1^2+A2^2)/(2*A2)
Si en A1 tu as la largeur et pas la demi largeur, dans la formule que je viens te te donner, tu remplaces A1^2 par (A1/2)^2
je me disai bien que tout n'était pas clair dans mon énoncé, en tout cas.... ca fonctionne tres bien meme apres une deuxieme verification avec d'autre dimensions, trop cool , merci....
mais je vais essayer d'être plus clair....
en fait je veux définir le cercle qui correspond au cintre d'une fenetre ou d'une porte.
ca correspond a la partie arrondie de la maconnerie en partie haute.
donc je mesure la largeur de la porte à la base du cintre qui me donne la cote appelée d et la hauteur entre cette base et le point le plus haut de la maconnerie qui me donne la cote h et voila!!
jusque la , je récupérais mon rayon avec un compas, le calcul est bien plus pratique....
cool on peut meme dessiner....
en fait ma hauteur est en ce qui me concerne toujours au milieu de ma base AB, ma hauteur , formant le petit coté de deux triangle rectangles égaux
maintenant je vais de ce pas, inscrire tous cela dans mon tableur.
merci encore , ca va bien me s'implifier la vie.
bonne soirée a tous



 géométrie en post-bac
géométrie en post-bac