Bonjour

Il faudrait lire avant de poster,  car  vous devez recopier le texte
et d'autre part  

1 exercice = 1 sujet

il y aurait donc dû y avoir 3 messages  

Autre remarque : il faudrait mettre à jour votre profil

Bonjour :
enfaite je n'arrivai pas a recopier correctement les exercices avec les symboles mathématiques c'est pour cela que j'ai penser que ce serai plus clair si je mettais directement ma feuille voila et je n'avais pas vu que un sujet = un exercice désoler

je ne sais pas comment mettre a jour le profil je suis débutante sur le forum

Pour mettre à jour votre profil  cliquez sur le pseudo espace membre
vous avez alors une page avec mon compte et le premier item est mon profil

pour taper des textes mathématiques vous avez l'aide au latex ou où vous trouverez



Recopiez le premier exercice  à la suite de ce message en y répondant

D'accord merci je regarderai après

exercice 1 :
Soit la suite (un) définie par u0=1 et un+1=2un+1

1. Démontrez par récurrence que , un<un+1
je ne sais pas


2. Que peut on dire de la suite (un) ?
On peut dire que la suite (un) est décroissante

Bonjour,
leilaserad, tu n'es pas nouveau sur l'île.
Je m'étonne que tu ne connaisses pas ses règles.
Je t'invite à lire A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien).
Le point 2 renvoie en particulier à

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

On vous demande de montrer que


initiation  

en supposant que montrez alors que


Si vous montrez cela, c'est bien dire que la suite est croissante

Et mets à jour ton profil.

oui je ne viens pas d'arriver sur ce forum mais j'ai dit que j'était nouvelle car je n'ai utiliser ce forum que 1 ou 2 fois . Je ne connais donc pas très bien les règles du forum je m'en excuse

Maintenant changez votre profil sinon je ne pourrais continuer

j'ai essayer de le changer mais ca ne veut pas marcher les donner ne veulent pas ce remplacer

je crois que c est bon mon profil est changer

Maintenant, c'est fait.

Que proposez-vous ?

Oui, ton profil est changé.

u0<u1
un-1<un on fait +1 des deux cotés ducout ca fait :
un<un +1 mais je ne comprend pas pourquoi la suite est croissante car le signe est du coté décroissant

et on a bien

Il ne faut pas confondre

Dans le premier cas on ajoute 1 à
dans le second cas on prend le successeur de dans la suite

donc ca c'est pour l'initialisation c'est ça ?

et pour l'hérédité comment faire ?

Oui, c'est bien pour l'initialisation  
Vous voyez bien que la suite ne peut être décroissante

montrez que

un-1<un il ne faut pas faire +1 des deux cotés ? et donc ca donne
un <un+1

Non, vous n'avez pas fait attention à ma remarque

on va construire le successeur

hypothèse de récurrence

on a le droit de multiplier les deux membres d'une inégalité par un même réel strictement positif



on peut ajouter un même nombre



maintenant on peut prendre la racine carrée. Cette fonction est croissante sur

Vous continuez

hérédité : supposons que jusqu'a un entier k ( il faut remplacer par k non  ? )
uk-1<uk
2uk-1<2uk
2uk-1+1<2uk+1
ca fait 2uk<2uk+1

c'est ça ?

Il faudrait écrire correctement les indices  vous mélangez les indices et les nombres

ce que vous avez écrit






ensuite cela ne va plus, car vous prenez le 1 de l'indice pour l'additionner avec le 1

Là on va plutôt prendre la racine carrée

, car   croissante  sur

là on reconnaît   et



On a donc montré que la propriété étant vraie pour elle est vraie pour

donc

Ah d'accord merci beaucoup et donc c'est  fini pour l'hérédité ? et ducout comment conclure?

Soit la propriété

On a montré que était vraie  puis, que entrainait   par conséquent pour tout est vraie

Et ducout pour la question 2 on peut dire que la suite est décroissante c'est ça ?

Et ça ducout c'est juste :
u_{k-1}<u_k

2 u_{k-1}<2u_k

2 u_{k-1}+1<2u_k+1

Du coup
le message de 21 :34 reprend les 3 premières lignes du message de 20:58
en mieux écrites et que j'avais approuvées à 21:14

Non la suite n'est pas décroissante  elle est croissante,  c'est même la définition d'une suite croissante
Les dix premiers termes de la suite en valeurs approchées


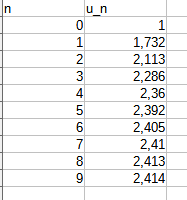
Vous pouvez bien constater que la suite est croissante

a oui voila désoler je reprend ce que je voulais dire ducout dans l'hérédité est-ce que ca c'est juste :
uk-1<uk
2uk-1<2uk
2uk-1+1<2uk+1

et comment justifier que la suite est croissante il faut utiliser u0,u1,u2 par exemple pour montrer que c'est croissant ?

Bonjour,
Je réponds en l'absence de hekla.
Ce que tu as écrit est illisible.
Utilise le bouton "X₂" pour les indices, et fais "Aperçu" avant de poster.

Quelle est la définition d'une suite croissante ?

Bonjour :

u_k-1 <u_k
2u_k-1<2_uk
2_uk-1+1<2_uk+1

C'est ça ?
et une suite croissante est Une suite est croissante si chaque terme est supérieur ou égal à son précédent : un+1 ≥ un donc on peut dire que c'est une suite croissante car , u_n<u_n+1 c'est ca ?

Reprenez les différents messages
il y a les réponses à vos interrogations

hérédité

on suppose que pour l'indice on a

  on veut alors montrer que cela entraîne


question 2 on connaît la définition d'une suite croissante et on dit que cette suite y répond

_{Sylvieg edit : Indice k-1}

Reprenons le tout

hérédité

on suppose que pour l'indice on a

  on veut alors montrer que cela entraîne

Par hypothèse de récurrence

on multiplie les deux membres de l'inégalité par 2



On ajoute 1 aux deux membres

  #  tout ceci correspond bien à vos trois lignes

On prend maintenant la racine carrée de chaque terme.   est une fonction croissante




En reprenant la définition de la suite on a

Conclusion  21:31

question 2  on peut ajouter strictement  votre réponse est plus correcte qu'avant

Une suite est strictement croissante si pour tout

on a montré que la suite vérifiait cette relation par conséquent,  c?est une suite strictement croissante

_idem

ducout pour l'hérédité ça va donner :

Supposons que k jusqu'à un entier k
u_k-1 <u_k
2_k-1<2_uk
2_uk-1+1< 2_uk+1
2_uk-1+1<2_uk+1 car xx croissante sur +

la on reconnait u_k et u_k+1
2_uk-1+1<2_uk+1

On a donc montré que la propriété étant vraie pour k elle est vraie pour k+1 donc , u_n<u_n+1

question 2 : que peut on dire de la suite u_n?
On peut dire que la suite est croissante  si chaque terme est supérieur ou égal à son précédent : un+1 ≥ un donc on peut dire que c'est une suite croissante car , un<un+1

Est-ce que tout ça est juste pour l'exercice 1

et pour la conclusion c'est ça :
Soit p(n) la propriété u_n<u_n+1

On a montré que p(0)  était vraie  puis, que p(n) entrainait p(n+1)  par conséquent n,  p(n) est vraie

du coup pour l'hérédité ça va donner :

Supposons que k jusqu'à un entier kla propriété est soit vraie au rang k
u_k-1 <u_k
2u_k-1<2u_k
2u_k-1+1< 2u_k+1
(2u_k-1+1)<(2u_k+1) car xx croissante sur R₊

là on reconnait u_k et u_k+1
(2u_k-1+1)<(2u_k+1)

u_k<u_k+1

On a donc montré que la propriété étant vraie pour k elle est vraie pour k+1 donc n N, u_n<u_n+1
Pour la conclusion
Soit p(n) la propriété u_n<u_n+1
On a montré que p(0)  était vraie  puis, que p(n) entrainait p(n+1)  par conséquent n,  p(n) est vraie soit n N, u_n<u_n+1

question 2 : que peut on dire de la suite u_n?
On peut dire que la suite est croissante  si chaque terme est supérieur ou égal à son précédent : u_n+1 ≥ u_n donc on peut dire que c'est une suite strictement croissante car, u_n<u_n+1

Est-ce que tout ça est juste pour l'exercice 1  Oui avec les quelques rectifications faites

Vous vous êtes un peu mélangé dans l'écriture des indices

d'accord merci beauoup vous pouvez m'aidez aussi pour l'exercice 2
Voici l'exercice :
Soit la suite (u_n) définie par u₀=4                                
                             u_n+1=2u_n² +1

Démontrons par récurrence que la suite (un) est positive

Il faudrait faire davantage attention

on vous a dit  1 exercice =1 sujet

par conséquent, je vais faire comme si vous n'avez pas posté le texte

Ouvrez un nouveau sujet et écrivez le texte de l'exercice 2 uniquement

puis, un autre où vous écrirez le texte de l'exercice 3

Remarque : quand 2 verbes se suivent le second est à l'infinitif  : aider

sébon je l'ai poster et merci

Je ne parlais pas d'auxiliaire