Inscription / Connexion Nouveau Sujet
complément sur les suites
Bonjour à tous,
Je rencontre un petit problème avec un exercice qui est le suivant:
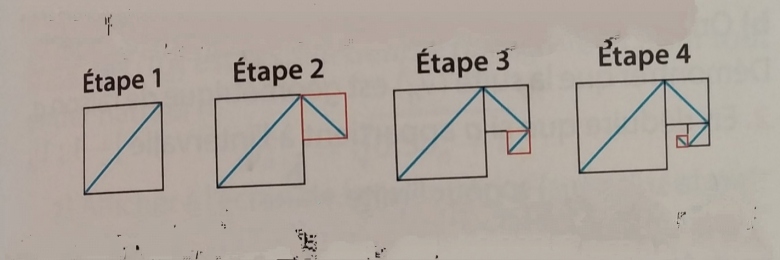
On construit une spirale en disposant bout à bout des diagonales d'une suite de carrés. A chaque étape, le côté du carré est divisé par 2; à l'étape 1, il est égal à 1.
(Je m'excuse je n'ai pas réussi à charger l'image du schéma de la spirale)
On note Ln la longueur de la spirale à l'étape n, avec n≥1. Ainsi, Ln=√2.
1.a. Expliquer pourquoi la suite (Cn) des côtés des carrés successifs est géométrique. Préciser sa raison.
On constate que d'étape en étape la longueur du côté est toujours divisé par 2. Or on sait que diviser par deux équivaut à multiplier par son opposé 1/2. Donc à chaque étape on multiplie le coté précédent par 1/2. Il existe donc une réel q constant. La suite (Cn) est donc géométrique. Et sa raison est don 1/2
b. Exprimer Cn en fonction de n
Cn=2*(1/2)n
2.a. Exprimer Ln en fonction de C1,C2,...,Cn.
Je n'arrive pour le moment pas à trouver comment exprimer Ln.
b. Justifier que pour tout entier naturel n≥1,
Ln= 2√2(1-(1/2)n).
J'ai supposé que ici il fallait utiliser la récurrence. J'ai réussi à faire l'initialisation:
L1=√2
2√2(1-(1/2)1)=√2
Donc P(n) est vrai à un rang k=1.
Cependant je n'arrive pas à faire l'étape de l'hérédité.
c. Déterminer la limite de la suite (Ln).
lim 1=1
lim 1/2=1/2
lim (1/2n)=+00 (plus l'infini)
lim 1-(1/2)n=-00 (moins l'infini)
lim 2=2
lim √2=√2
lim2√2=2√2
lim 2√2(1-(1/2)n)=-00
La limite de (Ln) est donc moins l'infini (-00)
3.a. Écrire un algorithme afin de déterminer le rang n à partir duquel 2√2-Ln<10-p (avec p élément de N).
b. Coder cet algorithme en langage Python, le saisir et l'exécuter avec p=6.
Pour la question 3 je n'ai jamais eu affaire à des questions comme celle ci et je ne sais donc pas faire. De plus je n'ai pas de leçon à ce sujet auquel je pourrais me référer.
Pourriez vous m'aider pour la question 2.a et b ainsi que la question 3 ? Si jamais vous trouvez des erreurs dans les autres questions je suis ouverte à vos corrections.
Merci d'avance pour votre aide.
bonjour,
je n'ai pas tout regardé mais déjà, au début tu écris Ln =  2, ce serait pas plutot L1 =
2, ce serait pas plutot L1 =  2 ??
2 ??
ensuite, la suite est géométrique, c'est vrai, et sa raison est = 1/2 (qui n'est pas l'opposé de 2, mais l'inverse de 2)... et de premier terme ? que vaut C1 ?
rectifie ta réponse pour la question pour la 1b)
au début tu écris Ln =
 2, ce serait pas plutot L1 =
2, ce serait pas plutot L1 =  2 ??
2 ??
En effet autant pour moi il s'agit d'une faute de frappe.
Pour la question 1.b.
Cn=2*(1/2)n et a pour premier terme C1=2*(1/2)1=1
bonjour,
1a) c'est ici que tu dois préciser le 1er terme.
(Cn) est une suite géométrique de raison 1/2 et de premier terme C1=1.
1b) vu la réponse à la question 1a), je ne vois pas pourquoi tu écris Cn=2*(1/2)n... ce n'est pas faux mais tu pourrais aussi écrire:
Cn = (1/2)n-1
2a)
Ln c'est la somme des diagonales D1 à Dn
Ln = D1 + D2 + D3 + ....... + Dn
exprime D1 en fonction de C1, D2 en fonction de C2, et donc Dn en fonction de Cn.
vas y !
OK,
et donc en factorisant par  2, tu obtiens
2, tu obtiens
Ln =  2 (C1 + C2 + C3..... + Cn)
2 (C1 + C2 + C3..... + Cn)
question 2a) terminée.
Passons à la suivante :
Justifier que pour tout entier naturel n≥1,
Ln= 2√2(1-(1/2)n).
pas besoin de récurrence, ici.
on a Ln =  2 (C1 + C2 + C3..... + Cn)
2 (C1 + C2 + C3..... + Cn)
la parenthèse est la somme des termes d'une suite géométrique (cf question 1).
Comment exprimes tu cette somme ? (ton cours te le dit)..
Ln = √2 (C1 + C2 + C3..... + Cn)
(C1 + C2 + C3..... + Cn) =C1*((1-qn-1)/(1-q))
Je me suis trompée
(C1 + C2 + C3..... + Cn) =C1*((1-qn)/(1-q))
Si le 1er terme de la suite est C1, alors:
Sn = C1 x (1-qn) / (1-q)
tu connais C1, tu connais q,
donc Ln = ???
mmhh..
n'attend pas pour réduire.. le "1* " est inutile, que vaut le dénominateur ? et tu as oublié le  2, etc....
2, etc....
Donc
Ln=√2(1-(1/2)n) / (1/2)
équivaut à Ln= 2√2(1-(1/2)n)
car diviser par (1/2) équivaut a multiplier par 2
Merci beaucoup. Maintenant il me reste plus qu'à faire la question 3.
En tout cas merci vous m'avez aider à comprendre et réussir.
euh... il te reste surtout à donner la limite de Ln ..
Evidemment, ça ne peut pas etre -oo : Ln est une longueur , comment pourrait elle tendre vers -oo ?
lim 1=1
lim 1/2=1/2
lim (1/2)n=+00 (plus l'infini)
lim 1-(1/2)n=+00 (n étant supérieur ou égal à 1)
lim 2=2
lim √2=√2
lim2√2=2√2
lim 2√2(1-(1/2)n)=+00
La limite de (Ln) est donc plus l'infini (+00)
non, ça n'est pas comme ça
tu te trompes quand tu dis que lim (1/2)n = +oo
reprends ton cours, prends un exemple, vérifie tes réponses.
je prends n=10 par exemple, penses tu que (1/2)^10 est très grand ?
donc quelle est la limite de (1/2)^n ?
ensuite, détailler lim 2V2 est inutile. 2V2 reste 2V2, c'est tout.
encore une fois, justbinet, vérifie tes réponses !!
Ln est une longueur, somme de diagonales, dont la première vaut V2, penses tu vraiment que quand tu vas ajouter un grand nombre de diagonales, la longueur totale va tendre vers 0 ???
tu es en terminale, tu devrais vérifier davantage ce que tu dis..
lim (1 - (1/2)n) .. tu dis que c'est egal à 0 ?
(1 - un truc presque egal à 0) ca tend vers 1, pas vers 0
donc
lim Ln = 2V2 * 1 = 2V2
OK ?
Pour la question 3 une autre aide extérieur m'a expliqué.Je te remercie en tout cas Leile pour m'avoir aider pour le reste de l'exercice.