Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale SimilitudesTopics traitant de similitudes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Composée de rotations de centres distincts

Posté par
Hagbou 13-03-12 à 16:29

Salut tout le monde.
Je suis actuellement en Terminale S, spécialité Maths.
J'ai un dm pour vendredi, le problème c'est que je suis réellement perdu, j'ai beaucoup de mal à comprendre le chapitre qu'il traite. Je vous expose l'exercice, ne me dites pas que je suis fainéant mais il n'y a vraiment aucune question à laquelle j'arrive à répondre... Je vous demande donc de l'aide s'il vous plait.


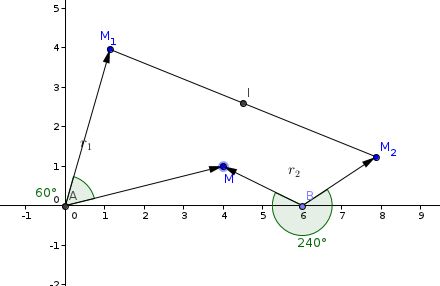
A et B sont deux points du plan orienté dans le sens usuel, tels que AB=6cm.
On note r1 la rotation de centre A et d'angle de mesure /3 et r2 la rotation de centre B et d'angle de mesure -2/3 .
Pour tout point M du plan, on note M1 et M2 les images respectives de M par r1 et r2 .

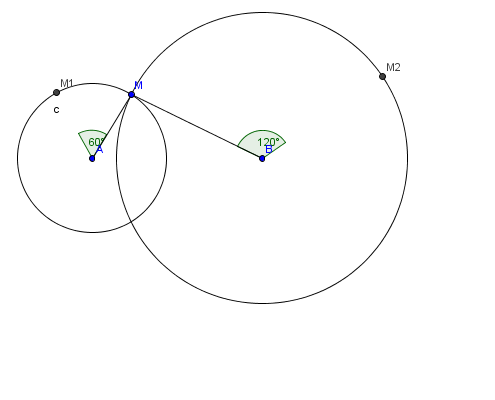
1. M étant un point du plan, construire les points M1 et M2.
2. Le but de cette question est de démontrer que, pour tout point M du plan, le milieu du segment [M1M2] est un point fixe I. On pose f= r1 o r2-1, où r2-1 désigne la transformation réciproque de r2.
  a. Déterminer f(M2)
  b. Montrer que f est une symétrie centrale
  c. En déduire que le milieu du segment [M1M2] est un point fixe I que l'on placera sur la figure
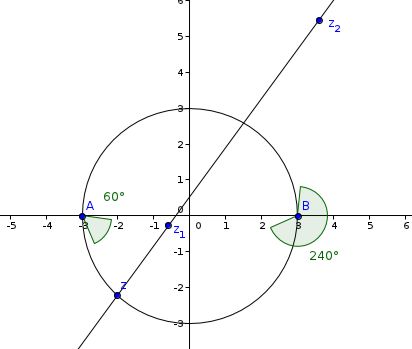
3. Dans cette question, le plan est muni d'un repère orthonormal direct (O ;  ;  ) tel que A et B aient pour affixes respectives -3 et 3. On note z1 et z2 les affixes respectives de M1 et M2. M est un point du plan, distinct de A et B, d'affixe z.
  a. Exprimer z1 et z2 en fonction de z. Montrer que :
(z2-z)/(z1-z)=i3(z-3)/(z+3)
  b. En déduire que :
- (MM1 ; MM2 ) = ( MA ; MB ) + /2 +2k  (ce sont des vecteurs)    (1) ;
- (MM2)/(MM1) = 3[(MB)/(MA)]  (2) .
  c. Déterminer, à l'aide de l'égalité (1), l'ensemble des points M du plan tels que M, M1 et M2 soient alignés. Construire sur la figure de la question 1.

Voilà, j'espère avoir une réponse de votre part. Je vous en remercie d'avance. Cordialement

Posté par
Hagboure : Composée de rotations de centres distincts 13-03-12 à 16:41

Je suis désolé, gros beug il manque pas mal de trucs ! j'arrive pas du tout a supprimer mon post pour le faire de nouveau ! je le fais donc a la suite .

Salut tout le monde.
Je suis actuellement en Terminale S, spécialité Maths.
J'ai un dm pour vendredi, le problème c'est que je suis réellement perdu, j'ai beaucoup de mal à comprendre le chapitre qu'il traite. Je vous expose l'exercice, ne me dites pas que je suis fainéant mais il n'y a vraiment aucune question à laquelle j'arrive à répondre... Je vous demande donc de l'aide s'il vous plait.


A et B sont deux points du plan orienté dans le sens usuel, tels que AB=6cm.
On note r1 la rotation de centre A et d'angle de mesure /3 et r2 la rotation de centre B et d'angle de mesure -2/3 .
Pour tout point M du plan, on note M1 et M2 les images respectives de M par r1 et r2 .

1. M étant un point du plan, construire les points M1 et M2.
2. Le but de cette question est de démontrer que, pour tout point M du plan, le milieu du segment [M1M2] est un point fixe I. On pose f= r1 o r2-1, où r2-1 désigne la transformation réciproque de r2.
  a. Déterminer f(M2)
  b. Montrer que f est une symétrie centrale
  c. En déduire que le milieu du segment [M1M2] est un point fixe I que l'on placera sur la figure
3. Dans cette question, le plan est muni d'un repère orthonormal direct (O ; ; ) tel que A et B aient pour affixes respectives -3 et 3. On note z1 et z2 les affixes respectives de M1 et M2. M est un point du plan, distinct de A et B, d'affixe z.
  a. Exprimer z1 et z2 en fonction de z. Montrer que :
(z2-z)/(z1-z)=i3(z-3)/(z+3)
  b. En déduire que :
- (MM1 ; MM2 ) = ( MA ; MB ) + /2 +2k  (ce sont des vecteurs)    (1) ;
- (MM2)/(MM1) = 3[(MB)/(MA)]  (2) .
  c. Déterminer, à l'aide de l'égalité (1), l'ensemble des points M du plan tels que M, M1 et M2 soient alignés. Construire sur la figure de la question 1.

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 16:49

1) as-tu réussi à construire les points M_1 et M_2 ?
2) que vaut r_2^{-1}(M_2}) ? que vaut r_2(M) ?

Posté par
malou Webmasterre : Composée de rotations de centres distincts 13-03-12 à 16:50

Bonjour

un coup de main pour démarrer

le dessin, je pense que je peux te laisser faire....

f=r1 ° r2-1
donc
f(M2) = r1 ° r2-1(M2)
mais tu commences par la "droite" et l'antécédent de M2 par r2 est M

donc il te faut
f(M2)=r1(M)

mais r1(M) vaut M1

donc f(M2)=M1

ensuite, la composée de deux rotations est une rotation d'angle la somme des angles
pi/3 -(-2pi/3) = pi

et une rotation d'angle pi est une symétrie centrale....

je te pense dépanné....

Posté par
Hagboure : Composée de rotations de centres distincts 13-03-12 à 17:01

@Dhalte, non je ne sais pas comment m'y prendre pour construire M1 et M2
@Malou merci pour l'aide, je vais essayer d'avancer

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 17:04

ça va être dur

Composée de rotations de centres distincts

Posté par
Hagboure : Composée de rotations de centres distincts 13-03-12 à 17:06

Merci pour le dessin mais je ne comprends pas , on a aucune coordonnée pour M !

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 17:08

tiens, en voilà un autre :
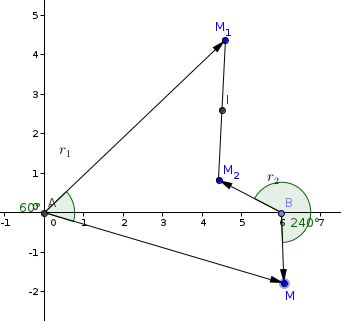
Composée de rotations de centres distincts
l'énoncé te demandait de choisir un point "quelconque", mais de préférence représentatif, et de construire ses images.

Posté par
malou Webmasterre : Composée de rotations de centres distincts 13-03-12 à 17:09

pas besoin

on fait tout avec cercles et angles

je faisais la même chose, dhalte....

Composée de rotations de centres distincts

Posté par
Hagboure : Composée de rotations de centres distincts 13-03-12 à 17:10

D'accord, merci pour la patience lol!

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 17:13

je ne sais pas ce que tu veux dire, malou, j'aidais simplement hagbou à répondre déjà à la première question...

Posté par
malou Webmasterre : Composée de rotations de centres distincts 13-03-12 à 17:14

....le"je faisais la même chose" était qu'on s'était mis tous les deux au dessin....

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 17:19

ahhhh

je croyais que ton expression "je faisais la même chose" se reportait au schéma que tu avais posté

et quand je parlais de point quelconque, ton choix de M semble le placer sur [M_1M_2], ce qui est un risque de mauvaise interprétation.

Posté par
malou Webmasterre : Composée de rotations de centres distincts 13-03-12 à 17:20

oui..je vois l'enchainement des posts..;et en réalité, mon "pas besoin" était une réponse à

Citation :
mais je ne comprends pas , on a aucune coordonnée pour M !
...mais tu as posté entre deux....

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 17:23


ça tourne au psychodrame.
étendez-vous ici, cher client, nous allons reprendre depuis votre tendre enfance.

bon, j'arrête mes délires, et je laisse la parole aux pros.

Posté par
Hagboure : Composée de rotations de centres distincts 13-03-12 à 17:36

Grâce a vos réponses j'ai fait la question 1 et la 2a.b.; quelqu'un a des idées pour la suite?

Posté par
malou Webmasterre : Composée de rotations de centres distincts 13-03-12 à 17:41

Citation :
c. En déduire que le milieu du segment [M1M2] est un point fixe I que l'on placera sur la figure


tu as donc une symétrie centrale qui transforme M1 en M2

habituellement, le centre de symétrie, il est où ?......

Posté par
dhaltere : Composée de rotations de centres distincts 13-03-12 à 17:42

le centre est au milieu ?

Posté par
Hagboure : Composée de rotations de centres distincts 13-03-12 à 17:42

Hmm bien vu.. j'ai honte, la spé maths : j'en fais des cauchemards

Posté par
Hagboure : Composée de rotations de centres distincts 15-03-12 à 20:07

Bonsoir, tout l'monde, j'en suis à la question 3c. j'ai reussi a exprimer z1 et z2 en fonction de z2 mais je n'arrive pas a trouver le résultat suivant. Help please!

Posté par
Hagboure : Composée de rotations de centres distincts 15-03-12 à 20:09

en fonction de z*.

Posté par
dhaltere : Composée de rotations de centres distincts 15-03-12 à 20:49

le cercle de diamètre [AB]
Composée de rotations de centres distincts

Posté par
Hagboure : Composée de rotations de centres distincts 15-03-12 à 20:50

Montrer que :
(z2-z)/(z1-z)=i3(z-3)/(z+3)
c'est la que je suis bloqué Dhalte...

Posté par
Hagboure : Composée de rotations de centres distincts 15-03-12 à 20:51

J'ai fait une erreur j'ai dis 3c mais c'est a 3a que je suis .. désolé

Posté par
dhaltere : Composée de rotations de centres distincts 15-03-12 à 22:46

rappels :
soient \vec u et \vec v deux vecteurs non nuls d'affixes respectifs u et v

leurs normes sont égales aux modules des affixes
||\vec u||=|u|

||\vec v||=|v|

et plus intéressant en ce qui nous concerne, l'angle

si \alpha est l'angle orienté entre le vecteur directeur de l'axe des abscisses et \vec u, alors nous avons

u=|u|(cos(\alpha)+i\sin(\alpha))=|u|e^{i\alpha}

si \beta est l'angle orienté entre le vecteur directeur de l'axe des abscisses et \vec v, alors nous avons

v=|v|(cos(\beta)+i\sin(\beta))=|u|e^{i\beta}

Mieux encore :

si \gamma est une mesure de \widehat{(\vec u,\vec v)}, alors \gamma = \beta - \alpha\mod 2\pi (fais un graphique si ça te surprend)

et pour faire le lien avec les complexes :
\frac vu=\frac{|v|}{|u|}\dfrac{e^{i\beta}}{e^{i\alpha}}=\frac{|v|}{|u|}e^{i(\beta-\alpha)}

Il y a un lien fort entre les angles des vecteurs et les arguments de leurs affixes

donc z_1 est l'image de z par la rotation de centre A, d'angle \frac{\pi}3

si a est l'affixe de A, alors en posant :
u=z-a

v=z_1-a
on a alors \widehat{(\vec u,\vec v)}=\frac{\pi}3\mod2\pi

et d'après ce qu'on vient de voir :
\frac{z_1-a}{z-a}=e^{i\gamma}

et donc
z_1-a=e^{i\frac{\pi}3}(z-a)

z_1=e^{i\frac{\pi}3}(z-a)+a

maintenant, a=-3 dans ton énoncé

z_1=e^{i\frac{\pi}3}(z+3)-3

de la même manière
z_2=e^{i\frac{-2\pi}3}(z-3)+3

Etape suivante : il te faut montrer que
\dfrac{z_2-z}{z-1-z}=i\sqrt3\dfrac{z-3}{z+3}


Rechercher
Menu
Espace membre
8 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !