Inscription / Connexion Nouveau Sujet
composée de similitude
BONJOUR.
Je fais un exercice sur les similitude dont voici l'énoncé : A et B deux points distinct.
rA et Rb sont les rotations ce centre respectif A et B et d'angle pi/2.
pour tout point M du plan, M1 et M2 sont les images respectives de M par rA et rB.
on note t la transformation rBorA-1
1a. construisons le point C=t(A)
b.determinons la nature et les éléments de t ( ça je sais , c'est une translation de vecteur AC )
c. quel est la nature dy quadrilatère M1M2CA ? (moi je trouve que c'est une droite mais je dois mettre trompé)
merci de votre aide.
merci mais maitenant je bloque a une autre question ; M decrit le cercle de diametre AB . determinons et construisons le lieu I , milieu du segment M1M2 quand M decrit le cercle de diametre AB. je pense que I décrit aussi le cercle de diametre AB mais je ne vois pas comment l'expliquer
d'accord mais comment je l'explique mathematiquement?
Bonjour,
Je suis désolé le dessin précédent est faux.
L'angle de la rotation rB est -pi/2
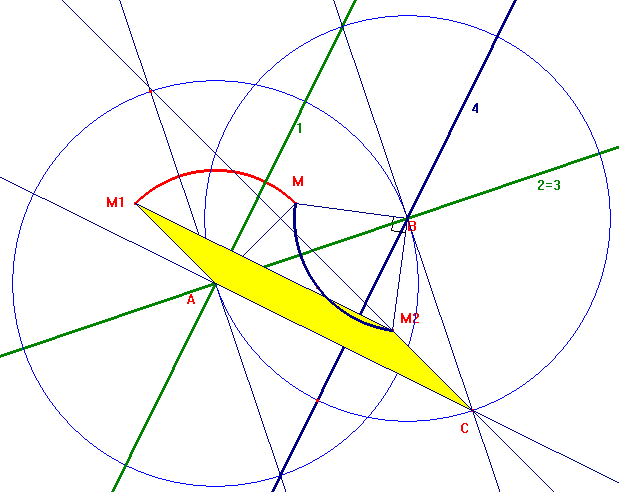
Le vrai dessin est le suivant:
Le lieu du point I est bien le cercle de diamètre [AB].
On doit pouvoir démontrer cela facilement par les affixes( mais ce n'est pas mon domaine).
voir
tout ce qu'il faut savoir sur les nombres complexes pour les rotations.
Soit A=(-1,0) , B=(1,0), M=cosµ + i.sinµ
Exprimer
.z1=image de M par la rotation de centre A et de pi/2;
.z2=image de M par la rotation de centre B et de pi/2
Trouver I'=(z1+z2)/2
On devrait trouver que I' a un module de 1.(appartient au cercle)
Si je me suis permis de répondre, c'est que votre message n'avait pas reçu de réponse.
J'espère que ceci pourra vous aider.
La suite est pour d'autres GM plus fort que moi.
@+ Caylus
Re,
Soit O, le milieu de [AB]
En regardant le dessin, on voit que l'angle NOI2=90°.
Soit A=(-1,0) , B=(1,0), (A+B)/2=(0,0) le point O.
z2=i(z-B)+B
z1=i(z-A)+A
I=(A+B)/2=(z2+z1)/2=i/2.(2z-B+A)+(B+A)/2=i.z cqfd.
bonjour, j'ai le même exercice à faire et je n'arrive toujours pas pour la question 1c à prouver qu'il s'agit d'un parallélogramme. de même pour la dernière question sommes nous obliger de passer par les affixes? merci de me répondre assez rapidement
Annuler
connectez vous