Inscription / Connexion Nouveau Sujet
Composées de transformation
Bonjour! J'ai un devoir maison de spécialité math à rendre pour lundi et je bloque sur la dernière question du dernier exercice, dont voici l'énoncé :
"On considère deux point A (3; -1) et B (0; 2). On désigne par h l'homothétie de centre A et de rapport -V2 ; r la rotation de centre B et d'angle 3pi/4 ; t la translation de vecteur BO."
a) construire le point oméga du plan dont l'image par toroh est l'origine O.
J'ai réussi cette question.
b) quelle est la nature de la transformation t o r o h? En donner les caractéristiques.
Par définition, j'ai toroh est une similitude de rapport V2 (c'est en effet la composée d'une isométrie avec une homothétie, son rapport est donc la valeur absolue du rapport de l'homothétie)
Ensuite, il m'a semblé que son angle est 3pi/4 mais j'ai du mal à l'expliquer, ça me semble se déduire directement de l'énoncé.
Mais c'est le centre qui pose problème. J'ai utilisé plusieur théorème dont AL-kashi qui se sont révélés inefficaces pour calculer ses coordonnées.
Une piste que je n'arrive pas à exploiter est donnée par l'énoncé : "Considérer les points M et N tels que h(N) = M et r (M) = N."
Merci de me répondre
PS : nous n'avons pas vu les complexes pour l'instant
Bonsoir,
j'ai toroh est une similitude de rapport V2
Oui.
il m'a semblé que son angle est 3pi/4
Non, une homothétie de rapport négatif est une similitude directe d' angle
Si bien que la similitude directe
Du coup, en appelant
Autrement dit, le triangle
Tu as construit
Il reste à construire le triangle
Je n' ai pas utilisé l' indication de ton énoncé; remarque que, avec
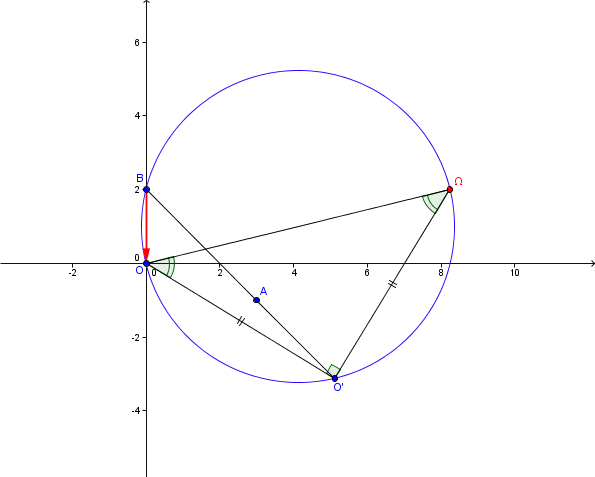

Merci bcp pour la réponse, effectivement le centre est bien trouvé.
Il reste cependant certaines choses que je ne comprends pas.
Comment déduit-on que l'angle est 3 /4-
/4- ?
?
En fait la question est plutôt de savoir comment le prouver?
Et enfin, dois-je calculer les coordonnées de ce point maintenant que je l'ai trouvé?
Encore merci pour la réponse qui est à la fois simple et claire.

L' angle de la composée de 2 similitudes directes d' angle et
est
Cela figure dans le cours...
Et enfin, dois-je calculer les coordonnées de ce point maintenant que je l'ai trouvé?
Possible; il s' agit de répondre à ceci:
En donner les caractéristiques.
Pour info

Je viens de regarder mon cours et ça n'y figure pas, il ne faut pas chercher plus loin la raison pour laquelle l'exercice semblait si dur... Et d'accord je vais calculer les coordonnées.
Bon fin d'après midi et merci beaucoup


