S'il vous plait j'ai vraiment besoin d'aide
Quelqu'un pourrait m'aider a comprendre? merci!

Bonjour,

J'ai calculé FE et je trouve 5.9 cm
Pour le cote FC je trouve 9.5 cm et pour le cote ce je trouve 15.3 cm
Je sais pas si c'est bon. Pour la conjecture je pensait a supposer le triangle rectangle parce que dans la derniere question du DM ils nous disent "supposons maintenant que les points E, C et F soient alignés
d'après le theoreme de Thales...
Finir le raisonnement et conclure."
donc c'est completement debile de faire deux fois la meme chose c'est obligatoirement le triangle rectangle dans ce cas non?  

et aussi pour une des questions, j'ai calculer des angles comme ils me demandaient mais je ne sais plus comment les convertir en degres avec la calculette apres :S

Est-ce que tu peux mettre l'énoncé exact du début à la fin stp ?

Ouaip
Tracer un carré ABCD de côtés 8 cm.
E est le point de la demi-droite [AB) tel que BE= 13 cm.
F est le point de la demi-droite [AD) tel que DF= 5 cm.
1) Emettre une conjecture quant aux points E, C et F.
2) On se propose d'examiner cette conjecture de trois manieres differentes:
a) Calculer FE, calculer de meme FC et CE.
Conclure.
b) Calculer les angles DCF et ECB.
Conclure.
c) Calculer l'aire du triangle FAE, puis la somme des aires de ABCD, BCE et DCF.
Conclure.
3) Que peut-on dire de la conjecture faite a la vue du dessin?
4) Raisonnement par l'absurde :
Supposons que les points E, C et F sont alignés,
d'apres le theoreme de Thales...
Finir le raisonnement et conclure.

Merci

1) Les points E, C, F ont l'air d'être alignés.

Avant toute chose, qu'on soit clairs sur le but de l'exercice :
La figure :

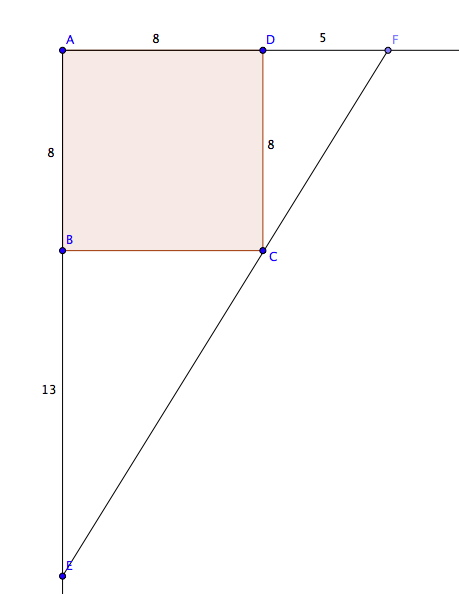
(j'ai tracé le segment [FE])
Un zoom vers le point C donne :

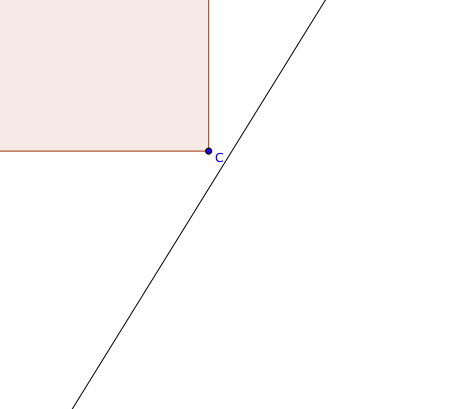
Donc, les points F, E, C ont l'air alignés de loin, mais en fait ils ne le sont pas (C n'est pas sur [FE]). Ce qu'on va montrer dans la suite de l'exercice, c'est donc que notre conjecture en 1) était fausse.

2) a) Mieux vaut laisser les valeurs exactes !
FC=√89 (environ 9,5)
CE=√233 (environ 15,3)
Re-calcule FE, si tu trouves 5,9 il y a un problème : FE serait plus petit que FC ?
Je trouve FE=√610 (environ 24,7).
--> Si les points étaient alignés, alors on aurait FE=FC+CE (autrement dit FE-FC-CE=0). Prends ta calculette et regarde si ça fait 0 ou pas (avec les valeurs exactes !).

Tel que j'ai fait ma figure FE est censer etre plus petit que FC en fait!
he hum jai fait le calcul et je trouve -1.40584074e^-4   oups

Pour convertir des radians en degrés pas besoin de calculette, c'est de la proportionnalité

Mettons que je veuille savoir combien 3,5 radians font en degrés :

pi radians  <-> 180°
3,5 radians <-> x degrés ?

x=180*3,5/pi = 200,53 environ --> 3,5 radians correspondent à un peu plus de 200,5 degrés

hoou je crois que c'est trop complique pour mon cerveau ça

Pour le carre du depart j'ai mis ABCD avec le B a la droite de A donc forcement toute la figure change et le point F est sur le segment AD plutot sortant de 5 cm en dehors du carre

Ce n'est pourtant pas si compliqué

Bon, je peux pas te dire où aller sur ta calculatrice, donc (clique sur la flèche entre "degré" et "radian" pour intervertir le sens de conversion)

Quand on dit "un carré ABCD" ça sous-entend toujours :

soit comme ceci : (on écrit les lettres en tournant dans le sens des aiguilles d'une montre)
A----------B
|            |
|            |
|            |
D----------C

soit comme cela : (dans le sens inverse des aiguilles d'une montre)

A----------D
|            |
|            |
|            |
B----------C

mais surtout pas "en croisant" comme ça :

A----------B
|            |
|            |
|            |
C----------D

Il faut vraiment que tu places tes lettres en "tournant autour du carré". On est d'accord, ou bien c'est là que ta figure a un problème ?

D'accord merci c'est bon. Je crois que sur la calculette il faut aller dans mode

Oooooooouf non non de ce cote la jme suis pas planter! mon carre est comme ta premire figure

hum j'ai calculer l'angle DCF et l'angle ECB et ils sont egaux. ça doit surement vouloir dire queque chose hein?

Je ne comprends toujours pas comment tu peux avoir FE plus petit que FC.
J'ai refait la figure avec ta configuration du carré (ça ne change rien). On n'a toujours pas la même ?

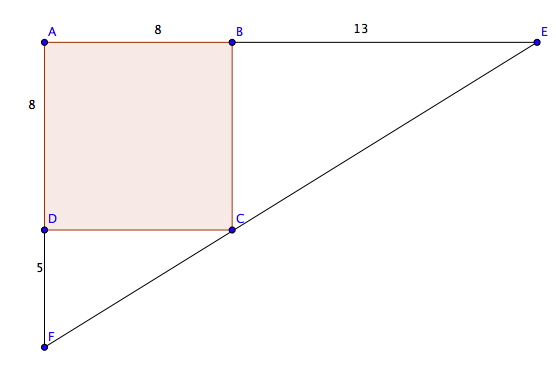
sisi c'est ça sauf que moi, j'ai place le point F sur le segment AD et le point B je l'ai mit dans l'autre sens donc il passe sur AB en fait (c'est peut etre pas bien de faire ça?)

"E est sur la demi-droite [AB)" signifie que E est sur le morceau de droite dessiné ci-dessous :

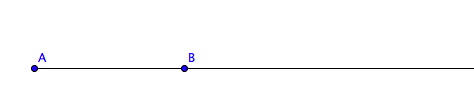
E ne peut pas être "à gauche de A".

Pour F l'énoncé est un peu ambigü, mais mets-le "à l'extérieur du segment" ; sinon, l'énoncé aurait plutôt dit "F est le point du segment [AD] tel que FD=5."

Pour le raisonnement par l'absurde,
je suppose que les points sont alignés d'apres le theoreme de Thales. Mais comment??

aie
alors je dois tout recommencer???  

J'ai refais les calculs et je trouve les meme resultat que tu m'avais dit

Tant mieux.

2)
a) FE≠FC+CE donc points pas alignés
b) Combien trouves-tu pour les angles, maintenant ?

Fe=√610
FC=√89
CE=√233

et pour la question 3)c) je trouve ^{136 cm}avec la figure bien dessinée

136cm² *

Pour le raisonnement je suis censer supposer que les points E,F,C sont alignés et donc de prouver qu'il ne le sont pas. J'utilise le theoreme de Thales et j'ai mis AD/AF = AB/AE = FC/FE
mais je ne sais plus comment prouver a partir de ça que les point ne sont pas alignés

aire de FAE = 136,5
somme des aires de ABCD, BCE et DCF = 136
on est d'accord ?

Ouaip c'est ce que j'ai trouver

Bin je sais meme pas si il y en a
peut etre FE//DB?

Aucune raison que (FE) et (DB) soient parallèles, a priori.

Bon, mais tu as quand même un carré, jusqu'à nouvel ordre les côtés d'un carré sont parallèles...

ho ha oui en effet maintenant qutu ldis..
mais je ne vois toujours pas comment prouver!

Supposons que les points E, C et F sont alignés,
d'apres le theoreme de Thales... --> écris les égalités données par Thalès (avec (BC)//(AF) par exemple, et remplace les longueurs que tu connais.
donc ...
Absurde.
Donc les points ne sont pas alignés.

c'est vrai? que ça? cool si c'est aussi simple les maths...

Oui
Bonne nuit !