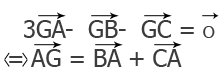Inscription / Connexion Nouveau Sujet
Construction d'un barycentre de 3 points
Bonsoir à vous,
Dans un premier temps, je souhaite à tous les membres de passer un agréable joyeux Noël et un bon réveillon.
Dans un second temps, je vous étaye mon problème, en fait un exercice m'est donné, je pense avoir compris, mais pas la globalité.
Je vais ne peut-être pas respecter la charte de l'énoncé en image.
Cependant, le soucis est qu'il y avait des signes grecs donc voilà je l'ai écrit sur Word 2010 et je vous l'envoie sus forme d'image.
Voilà ce que j'ai fait jusqu'à maintenant, en voici l'image, un dernier mot merci d'avance :
** image supprimée **
* Océane > dst même si il y a des symboles mathématiques, si tu veux de l'aide, merci de recopier ton énoncé sur le forum. *
étapes 3 et 4 ce n'est pas ça.
en 2/ on obtient :
G bary de (A; 3) (B; -1) (C; -1)
on pose I milieu de [BC]
G bary de (A; 3) (I; -2)
<=> AG = -2 AI
...
Je n'ai pas trop compris ton raisonnement, pourriez-vous détaillez un peu plus svp.
Et pourquoi prendre I milieu de [BC] et non pas [AC].
Et pour finir donc tous mon étape deux je peux la supprimer ?
ok. on reprend pas à pas.
Etape 1 :
a + b + c  0 donc le barycentre existe
0 donc le barycentre existe
Etape 2 :
MG = 3MA - MB - MC
-------- puisque c'est vrai pour tout M, c'est vrai si M = A
-------- on remplace M par A
AG = 3AA - AB - AC
AG = 3AA - AB - AC
AG = - (AB + AC)
------- on pose I milieu de [BC] --> AI = 1/2 (AB + AC)
AG = - 2 AI
...
Merci de ton explications, je vais essayer de continuer, mais je n'ai pas compris comment passe tu de ces deux lignes l'une à l'autre :
AG = 3AA - AB - AC
AG = - (AB + AC)
AG = 3AA - AB - AC
--------- le vecteur AA est nul
AG = 0 - AB - AC
AG = - AB - AC
-------- on factorise par -1
AG = - (AB + AC)
...
Désolé encore, mais il y a un soucis, car PGEOD utilise un certain point I, qui intervient dans un segment et dans un vecteur, et frankot non.
Rho je peux pas me retenir, d'après ce que j'ai compris, il faut suivre ce protocole pour ta figure frankot :
ABC est un triangle quelque conque.
On crée le point B' tel qu'il soit le symétrique de B par rapport à A et C' symétrique à C par rapport à A.
On trace les droites (BB') et (CC').
On crée une droite parallèle à (CC') passant par B' et une autre parallèle à (BB) passant par C'.
Le point d'intersection de ces droites, sera le point le barycentre G.
Nous savons que AG = BA + CA.
Je dis ça car j'en est 3 autres à faire encore, donc je me demande si ya pas plus cours.