Inscription / Connexion Nouveau Sujet
Construire centre d'inertie
Bonjour
J'ai besoin de votre aide pour résoudre l'exercice suivant ;
Construire le centre d'inertie de la plaque P obtenue en enlevant le disque de centre O' et de rayon r au disque de centre O de rayon R tel que R=3r
le dessin de la figure est attaché à ce message.
Merci d'avance de votre aide !
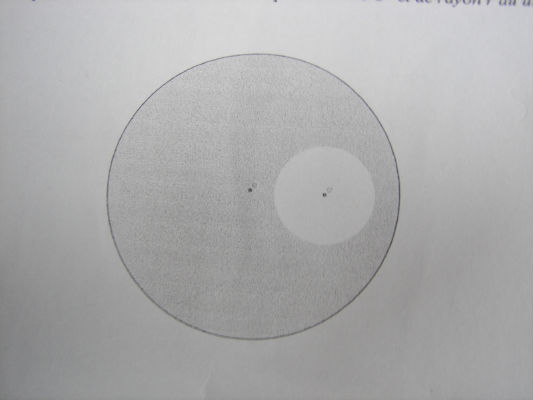
j'ai oublié de dire que le grand cercle est le O et le petit est O'
merci d'avance à ceux qui vont m'aider !!
Essaie d'écrire que le centre d'inertie de la plaque intégrale (non percée) est aussi celui du centre d'inertie de la plaque privée du disque et du centre d'inertie du disque seul placé au même endroit.
Bonjour
Le centre d'inertie G de la plaque trouée est le barycentre de (O; R²) et (O';-
R²) et (O';- r²)
r²)
(les plaques sont homogènes donc les masses sont proportionnelles aux surface... et le résultat se démontre grace à l'associativité du barycentre)
ou encore barycentre de (O;9) et (O';-1) dans le cas présent
petit plus :
dans le cas général, le fait que c'est le barycentre de (O;R²/r) et (O';-r) permet de construire G directement sur le dessin à la règle et au compas par la méthode suivante :
(C) est le grand cercle défini par O et R
(C') est le petit cercle défini par O' et r
sur la droite (OO'), soit A l'intersection de (C') avec (OO') qui n'est pas dans [OO']
et sur la demi-droite issue de O' passant par A, soit B tel que O'B=R
soit D tel que DAB rectangle en A, direct avec AD=R
soit (d) la demi-droite issue de O' dirigée par le vecteur v(AD)
soit E le point d'intersection de (BD) et (d)
soit (d') la demi droite issue de O dirigée par v(AD)
soit F le point de (d') tel que OF=r
la droite (EF) coupe(OO') en G
sauf erreur de ma part
MM


