Inscription / Connexion Nouveau Sujet
Convexité bis
Bonjour , pourriez-vous m?aider à faire cette exercice s?il vous plaît :
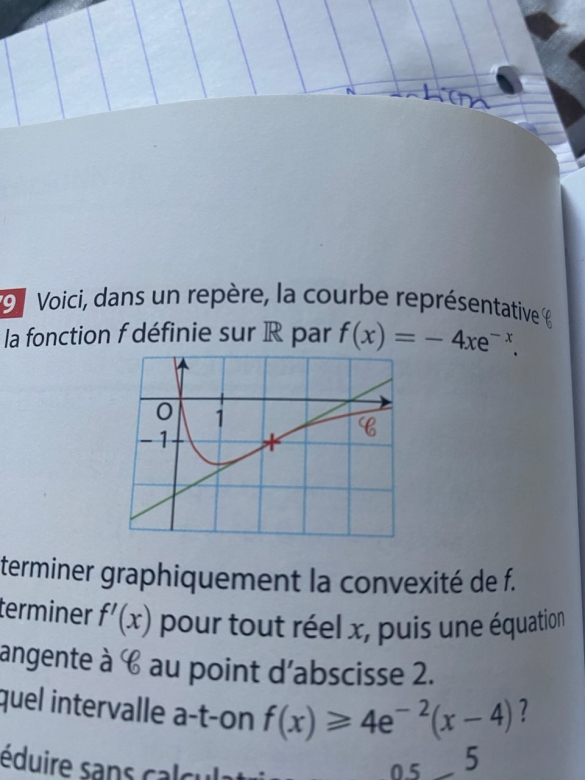
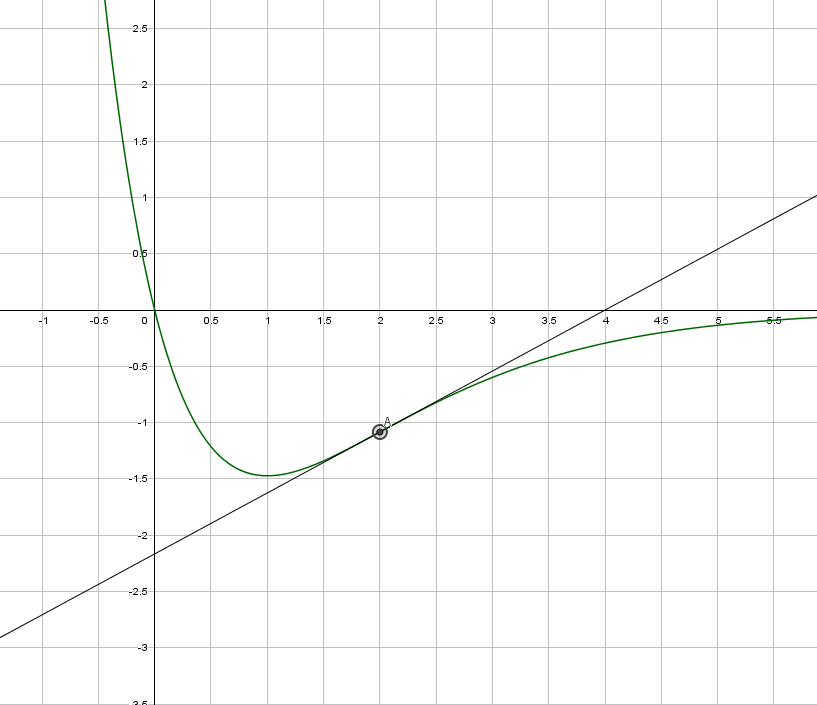
Voici, dans un repère, la courbe représentative C de la fonction f définie sur  par f(x) = -4e^-x.
par f(x) = -4e^-x.
a) Déterminer graphiquement la convexité de f.
b) Déterminer f?(x) pour tout réel x, puis une équation de la tangente à C au point d?abscisse 2.
c) Sur quel intervalle a-t-on f(x)  4e^-2(x-4) ?
4e^-2(x-4) ?
d) En déduire sans calculatrice que e^0,5  5/3. Le vérifier ensuite à la calculatrice.
5/3. Le vérifier ensuite à la calculatrice.
Bonjour,
Poste la courbe si tu veux de l'aide pour a).
Montre tes calculs pour cette question de b) :
Déterminer f'(x) pour tout réel x
Je ne vais plus être disponible ; mais d'autres intervenants vont passer

Pour la a) voici ma réponse : Alors pour la première question j'ai fais ça :
Graphiquement, entre ]- ;2], la fonction est convexe car la courbe de f est au dessus de la tangente. Et entre [2;+
;2], la fonction est convexe car la courbe de f est au dessus de la tangente. Et entre [2;+ [ la fonction est concave car la courbe est en dessous de la tangente.
[ la fonction est concave car la courbe est en dessous de la tangente.
Pour la b) f(x) = -4xe^-x
f'(x) = e^-x ( -4+4x)
Et pour l'équation de la tangente : y= f'(2) (x-2)+ f(2)
f'(2) = e^-2(-4+4x2)
f'(2)= e^-2(-4)
f(2)= -4x2e^-2
f(2)= -8e^-2
y= 4e^-2(x-2)+ (-8e^-2)
y=4xe^-2-8e^-2-8e^-2
y= 4xe^-2+(-16e^-2)
y= e^-2(4x-16) voici l'équation de la tangente
OK pour tes calculs.
note que tu pourrais factoriser davantage :
f'(x) = 4e^(-x) (x-1)
et pour la tangente y = 4e^(-2) (x-4)
ce qui nous amène à la question c)...
tu y vas ?
J'ai pas compris ce que vous trouvez ici , ou va le 16 y = 4e^(-2) (x-4) et ici aussi j'ai pas compris f'(x) = 4e^(-x) (x-1) est ce que vous pourriez m'expliquez s'il vous plaît
tu as écris f'(x) = e^-x ( -4+4x)
j'ai écrit e^(-x) pour bien montrer e-x
et (-4 + 4x) = 4(-1 +x ) = 4(x-1)
d'ou f'(x) = 4 e -x ( x-1) ==> f'(x) = 4e^(-x) (x-1)
pour l'équation de la tangente :
tu écris y = e^-2(4x-16)
et 4x - 16 = 4(x - 4) OK ?
je dois partir... je vais laisser un message pour qu'un autre intervenant puisse terminer avec toi. OK ?
-4xe^-x 4e^-2(x-4)
4e^-2(x-4)
-4x-1 4x-2-16-2
4x-2-16-2
-4x-4x e^0-18-2
e^0-18-2
-8x/-8 -21/-8
-21/-8
x 29
29
Est ce que c'est bon ? désolé du retard
Comment passez-vous d'une ligne à l'autre ?
Ne serait-ce pas plutôt une résolution graphique ?
Comment peut-on interpréter cette inéquation ?
Au vu des questions précédentes, vous pouvez répondre à la dernière question
est l'équation de la courbe
est l'équation de
On peut donc interpréter cette inéquation par : sur quel intervalle la courbe représentative de est-elle au-dessus de
est l'équation de la courbe
est l'équation de la tangente en 2 à la courbe .
On peut donc interpréter cette inéquation par : sur quel intervalle la courbe représentative de est-elle au-dessus de la tangente en 2 à la courbe représentative de
sur je ne pense pas que l'on puisse donner une autre réponse
Ok c'est à dire que on ne fais pas l'inéquation -4xe^-x 4e^-2(x-4) ? Mais comment on sait que c'est sur l'intervalle ]-
4e^-2(x-4) ? Mais comment on sait que c'est sur l'intervalle ]- ;2]
;2]
Bonsoir,
je n'aime pas trop cette question mais bon, une piste possible :
partir de l'inégalité précécente avec x = 3/2 = 1,5
Je crois que ça marche
Ou alors, en conservant des "x", voir d'abord que l'inégalité précédente équivaut à :
e-x+2  4/x - 1
4/x - 1
puis x = 3/2 = 1,5
Si je ne me trompe pas ......
bonsoir,
je suis d'accord avec co11
en partant de -4x e^-x < 4 e^-2 * (x-4)
on simplifie par 4, et on divise par e^-2 de part et d'autre
ca donne
- x * e^(2-x) < x-4
soit
x * e^(2-x) > x - 4
nous, on vise e^0,5
2 - x = 0,5 ==> x= 1,5
quand on applique x = 3/2 on a boutit bien à e^0,5 < 5/3 ... je crois 
j'ai fait une erreur (faute de frappe)dans le sens de l'ingalité ; je reprends :
en partant de -4x e^-x > 4 e^-2 * (x-4)
on simplifie par 4, et on divise par e^-2 de part et d'autre
ca donne
- x * e^(2-x) > x-4
soit
x * e^(2-x) < x - 4
nous, on vise e^0,5
2 - x = 0,5 ==> x= 1,5
quand on applique x = 3/2 on aboutit bien à e^0,5 < 5/3
Bonne soirée
decidemment, je devrais faire aperçu.. désolée !
en partant de -4x e^-x > 4 e^-2 * (x-4)
on simplifie par 4, et on divise par e^-2 de part et d'autre
ca donne
- x * e^(2-x) > x-4
soit
x * e^(2-x) < 4-x
nous, on vise e^0,5
2 - x = 0,5 ==> x= 1,5
quand on applique x = 3/2 on aboutit bien à e^0,5 < 5/3
Non
je ne comprends pas
ça donne
- x * e^(2-x) > x-4
soit
x * e^(2-x) < x - 4
Que devient le signe
Avec le correctif, d'accord
Ne faudrait-il pas dire que l'on est bien dans l'intervalle
oui, tu as raison hekla. Ce serait plus propre.