Inscription / Connexion Nouveau Sujet
Convexité et Coûts Totaux
Bonjour, j'ai un devoir maison composé de 3 parties à rendre à la rentrée. Ayant eu déjà un devoir surveillé sur le même chapitre auquel je n'ai pas compris grand chose. J'espère me rattraper sur celui-là. Merci par avance de votre aide.
Je mets ici seulement la première partie.
Le sujet : Un entreprise fabrique des objets et estime le coût total, en euros, de la production de x objets en fonction de x par : Ct(x) = x^3 - 60x^2 + 1500x + 5000 pour x
[0 ; 70]
On appelle les coûts fixes les coûts indépendants du niveau d'activité ou des quantités produites dont l'entreprise doit s'acquitter pour son bon fonctionnement (loyer, coûts administratifs etc.)
Le coût marginal est le coût supplémentaire induit par la dernière unité produite.
Mathématiquement, le coût marginal Cm est assimilé à la dérivée du coût total, Ct, par rapport à la quantité produite x.
A. Etude de coût total
1. Déterminer le montant en euros des coûts fixes.
2. Déterminer l'expression du coût marginal en fonction de x.
3. Déterminer les variations du coût total sur (0 ; 70)
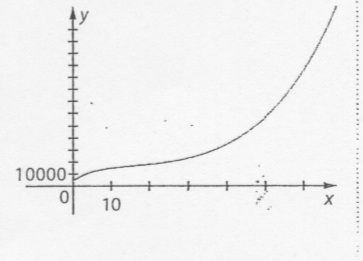
4. Voici la courbe C représentant Ct.
a. Quelle semble être la convexité de Ct
b. Afficher la courbe sur la calculatrice pour x entre 0 et 70 puis x entre 0 et 40
1) Le cout fixe est désigné par le prix hors fabrication. Donc même quand aucun objet est fabriqué. Donc quand x=0 
. Le coût fixe est de 5000€
2) il te suffit de dériver Ct . Tu sauras faire je pense
3) tu etudies avec la dérivée les variations. Si elle est positive alors Ct est croissante 
4) la convexité je n'ai pas encore entendu parler de sa dans mon programme de terminale :-S
Merci pour ta réponse.
Pour la première question, c'est bien ce que j'avais trouvé, ainsi que la deuxième. J'ai bloqué sur la 3e, j'ai fait la dérivé, ce qui m'a donné CT'(x)= 3x^2 - 120x + 1500 ; après j'ai fait delta et c'est là le problème j'ai trouvé -3600 et quand le delta est négatif il n'y a aucune solution alors comment je fais pour faire mon tableau de signe ?
On derive encore 6x -120.. Si la derivée de derivée c'est positif alors ta fonction sera croissante. Toujours pour f'' >0
C'est bon je viens de trouver 120/6 = 20 > 0.
Ce qui donne le tableau de signe
x 0 20 70
CT'(x) - +
Merci
A.1. couts fixes = 5000€
A.2. Cm(x) = Ct'(x) = 3x2-120x+1500
A.3. 
=(1202)-18000 = -3600 donc cette dérivée ne s'annule jamais, elle est donc toujours du même signe
donc Ct'(x) > 0 quel que soit x et en particulier x[0;70]
donc Ct(x) croit de Ct(0)=5000€ à Ct(70)=159000€
4.a. la courbe semble d'abord concave et ensuite convexe. ce qui signifie qu'il semble y avoir un point d'inflexion (point en lequel le sens de la courbure change).
pour le vérifier il faut calculer la dérivée seconde:
Ct"(x) = 6x-120 s'annule et change de signe en x=20
donc pour x[0;20[ c"(x) < 0 la courbe est concave
en x=20 C"(x)=0 donc changement de courbure en ce point: c'est un point d'inflexion
enfin pour x]20;70] c"(x) 0 la courbe est convexe
Bonsoir fred, merci pour tes réponses.
Ct(0) et Ct70) de la question A.3 représentent-ils le minimum et le maximum ?
Donc d'après ta réponse au 4.a le point d'inflexion est 20, là ou la courbe change de convexité.
Malgré l'heure tardive, je met la seconde partie. Au moins elle y sera déjà
B. Etude du coût marginal
1. Calculer la dérivée Cm en fonction de x
2. Déterminer le sens de variation de Cm sur l'intervalle (0 ; 70)
3. Justifier l'existence d'un point d'inflexion de C. Préciser l'abscisse de ce point.
4. a. A partir de quelle quantité produite, chaque objet supplémentaire produit est-il plus coûteux que l'objet précédent?
b. On appelle le rendement marginal le rendement prévu pour la production d'un objet supplémentaire.
Justifier l'affirmation suivante : "Pour une production de plus de 20 objets les rendements marginaux dans cette entreprise sont décroissants"
Pour la question 1, comme le Cm(x)=CT'(x) ; il suffit juste de mettre comme réponse D'après la question A.2 la dérivée est 3x^2 - 120x + 1500
Pour la question 2, le sens de variation signifie qu'il faut faire un tableau de signe et de variations ?
Cm'(x) c'est la Ct"(x) que j'ai calculé!
donc Cm'(x) = 6x-120 s'annule et change de signe en x=20
donc cm'(x) < 0 pour x[0,20[ donc Cm décroissante sur cet intervalle et décroit de Cm(0)=1500 à Cm(20)=300
et Cm'(x) = 0 pour x=20 donc Cm(20)=300 est le minimum
cm'(x) > 0 pour x]20,70] donc Cm croissante sur cet intervalle et croit de Cm(20)=300 à Cm(70)=7800
Merci pour ton explication Fred, j'ai réussi à comprendre ces 3 premières questions de cette seconde partie.
Pour la question 4.a faut-il entrer les fonctions dans la calculette ? Parce que je ne vois pas comment procéder avec la courbe qu'ils nous ont donnés.
bonjour j'ai le meme sujet mis a part que jai une troisieme partie auquel je n'ai rien compris, le voici:
Le cout moyen d'un objet lorsque x objets sont produits est donné par Cm(x)=Ct(x)/x pour x>0
1. quel est le cout moyen d'un objet pour 20 produits?
2.donner l'expression de Cm(x)
3.a. on note A le point de C d'abscisse x. Expliquer pourquoi Cm(x)est le coefficient directeur de la droite (OA).
merci d'avance
Annuler
connectez vous