Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Trigonométrie et fonctions trigonométriquesTopics traitant de trigonométrie et fonctions trigonométriques [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

cos(pi/5)

Posté par
Chamsi68 27-01-17 à 00:25

Bonjour,
J'ai pu aboutir à la valeur exacte de cos\left(\frac{\pi}{5}\right) en utilisant le polynôme de Tchebychev, qui est \frac{1+\sqrt{5}}{4}=\frac{\varphi}{2}, s'il vous plait, y a t-il une autre méthode permettant d'aboutir à ce résultat ? [niveau première]

Posté par
mathafou Moderateurre : cos(pi/5) 27-01-17 à 00:43

Bonjour,

si tu as besoin de cette valeur c'est sans doute qu'on te la demande dans un exo

quel est l'énoncé complet ? (mot à mot et pas "raconté")

la méthode est indiquée par la façon dont les différentes questions s'enchaînent
à mon avis les polynômes de Tchebychev ne sont pas au programme de Terminale (en France) alors encore moins en 1ère.
tu pouvais tout aussi bien ne rien utiliser du tout et trouver cette valeur directement "dans la littérature" (= sur Internet)
voire peut être même avec ces calculettes modernes qui font même le café (enfin presque).

Posté par
Chamsi68re : cos(pi/5) 27-01-17 à 01:10

Je ne suis pas un étudiant en France,
L'énoncé est le suivant :

On admet qu'il existe un polynôme T_{n} de degré n, (\theta \in IR) \cdot tel que : cos\left(n\theta\right)=T_{n}\left(cos\theta\right) \cdot
1) a) Vérifier que : T_{0}(x)=1, T_{1}(x)=x et T_{2}(x)=2x^{2}-1 \cdot
b) montrer que : (k \in )(\theta \in IR) : cos\left(\left(k+1\right)\theta\right)+cos\left(\left(k-1)\theta\right)=2cos\left(k\theta\right)cos\theta \cdot
c) Déduire que : (k \in IN^{\star}) T_{k+1}(x)=2xT_{k}(x)-T_{k-1}(x) \cdot
d) Déduire : T_{3}(x) et T_{4}(x) \cdot
2) a) Résoudre dans \left[0,\pi\right] : cos\left(5\theta\right)=0 \cdot
b) Résoudre dans IR : T_{5}(x)=0 \cdot
c) Déduire cos\left(\frac{\pi}{10}\right), puis cos\left(\frac{\pi}{5}\right) \cdot

Posté par
Chamsi68re : cos(pi/5) 27-01-17 à 01:15

On a travaillé l'Exo en classe, et on nous a affirmé que ça s'appelait le polynôme de Tchebychev, y a t-il une autre méthode pour aboutir à ce résultat ?

Posté par
mathafou ModerateurIE isocèle et que le trinagle 27-01-17 à 02:05

OK donc c'est bien ça qu'il faut faire pour faire l'exo.

après, il y a d'autres méthodes purement géométriques
considérer un décagone régulier, ou un pentagone

par exemple :

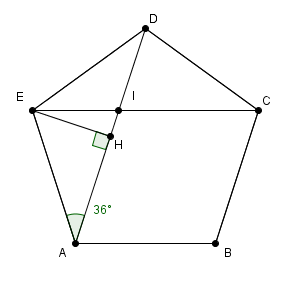
IE isocèle et que le trinagle

le triangle EID est isocèle et semblable au triangle AED

on en tire une relation entre AE et AD (prouver que le rapport AD/AE = φ le nombre d'or)
donc entre AE et AH donnant cos pi/5 = φ/2

Posté par
lakere : cos(pi/5) 27-01-17 à 10:03

Bonjour,

Une solution possible en 1ère pour le calcul de \cos\,\dfrac{\pi}{5}:

On montre que \cos\,3\theta=4\,\cos^3\theta-3\,\cos\theta

On a donc: \cos\,\dfrac{3\pi}{5}=4\,\cos^3\dfrac{3\pi}{5}-3\,\cos\,\dfrac{\pi}{5}=-\cos\,\dfrac{2\pi}{5}

4\,\cos^3\dfrac{3\pi}{5}-3\,\cos\,\dfrac{\pi}{5}=-2\,\cos^2\dfrac{\pi}{5}+1

Donc \cos\,\dfrac{\pi}{5} est solution de l' équation:

  4x^3+2x^2-3x-1=0

  (x+1)(4x^2-2x-1)=0

  \cos\,\dfrac{\pi}{5}\not=-1 donc \cos\,\dfrac{\pi}{5} est solution de:

   4x^2-2x-1=0

  Reste à  choisir entre les deux valeurs trouvées.

Posté par
lakere : cos(pi/5) 27-01-17 à 10:13

Evidemment une faute:

On a donc: \cos\,\dfrac{3\pi}{5}=4\,\cos^3\dfrac{\pi}{5}-3\,\cos\,\dfrac{\pi}{5}=-\cos\,\dfrac{2\pi}{5}

4\,\cos^3\dfrac{\pi}{5}-3\,\cos\,\dfrac{\pi}{5}=-2\,\cos^2\dfrac{\pi}{5}+1

Posté par
mathafou Moderateurre : cos(pi/5) 27-01-17 à 10:20

Bonjour,

??? (erreur de frappe en tapant du LaTeX et en se concentrant plus sur la syntaxe du LaTeX que sur le contenu mathématique)

ceci dit :
- encore faut il prouver en 1ère que \cos\,3\theta=4\,\cos^3\theta-3\,\cos\theta
et ce qui ne vient pas à l'esprit immédiatement de passer par 3/5 et 2/5 pour avoir du /5 !!

- aucune de ces méthodes alternatives de calcul n'est autorisée ici vu que l'exo est très précis sur la seule et unique exigée : suivre la logique de l'énoncé en répondant aux questions dans l'ordre telles qu'elles sont posées et pas à d'autres.

Posté par
lakere : cos(pi/5) 27-01-17 à 10:37

Bonjour mathafou

Il faut tout lire:

  

Citation :
s'il vous plait, y a t-il une autre méthode permettant d'aboutir à ce résultat ? [niveau première]


Posté par
mathafou Moderateurre : cos(pi/5) 27-01-17 à 11:43

c'est bien pour ça que je donnais aussi une méthode géométrique

je soulignais juste que ces méthodes ne peuvent en aucun cas servir à faire l'exo

c'est à dire à répondre à la question
2c) Déduire cos\left(\frac{\pi}{10}\right), puis cos\left(\frac{\pi}{5}\right)
autrement qu'en résolvant l'équation de la question 2b

mais on est parfaitement d'accord.

Posté par
Chamsi68re : cos(pi/5) 28-01-17 à 16:22

Merci beaucoup lake et mathafou, .


Rechercher
Menu
Espace membre
6 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1732 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !