AB (produits en croix)
Annuler
connectez vous
- Un petit Cours sur le cosinus - quatrième
- Trois Exercices sur le cosinus (différence entre un angle et son cosinus) - quatrième
- 10 Exercices sur les équations et les mises en équations - quatrième
- Six Exercices sur les pourcentages - quatrième
- Cours sur les fractions suivis de six Exercices - quatrième
- Exercice de Calcul avec des fractions - 4ème
- Les puissances - Cours 4ème
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième CosinusTopics traitant de cosinus [tout]Lister tous les topics de mathématiques
Niveau quatrième
Cosinus d'un angle aigu d'un triangle rectangle.
Posté par LoveIt
Bonjour,
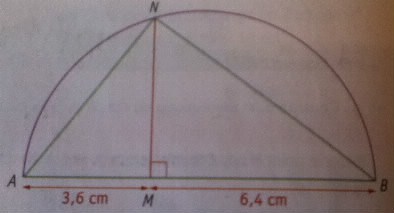
1) Construire en vraie grandeur la figure ci-contre dans laquelle:
- Le point M appartient au segment [AB];
- Le point N appartient au demi-cercle de diamètre [AB].
2) Déterminer la valeur exacte de AN.
3) En déduire une valeur approché de la mesure de l'angle BAN.
J'ai fait le 1), mais pour le 2) et le 3), je n'y arrive pas.
Merci à ceux et celles qui liront le topic.
AM²+MN²=AN²
3.6²+MN²=AN²
MN²=AN²-3.6²(1)
AB²=AN²+NB²
(3.6+6.4)²=AN²+NB² (2)
remplaçons MN² par l'expression (1)
NB²=NM²+MB²(2)
NB²=MN²+6.4²
NB²=AN²-3.6²+6.4² (3)
remplaçons (3) dans (2)
(3.6+6.4)²=AN²+NB²
10²= AN²+AN²-3.6²+6.4²
100=2AN²-28
72=2AN²
AN²=36
AN>0, AN=V36=6
prend le temps de relire
j'ai écrit le théorème de Pythagore dans les 3 triangles rectangles et j'ai exprimé tout en fonction de AN²