Inscription / Connexion Nouveau Sujet
Coupe d'un cube par un plan
Bonjour,
Voici l'énoncé de mon problème :
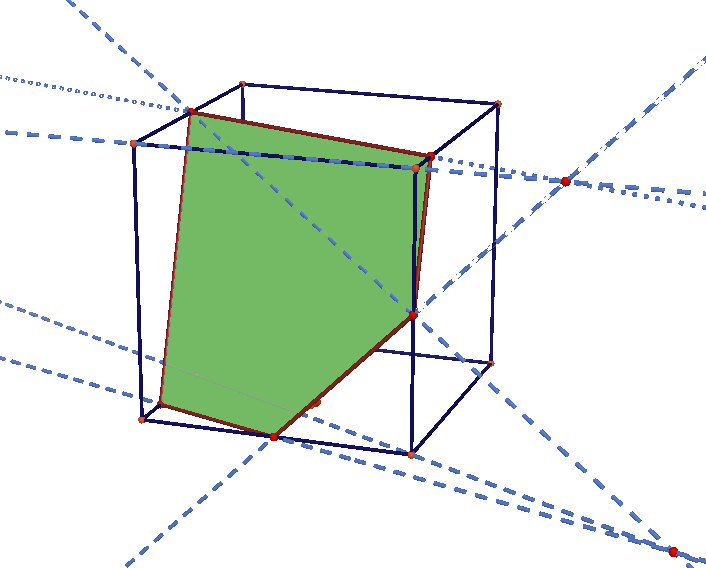
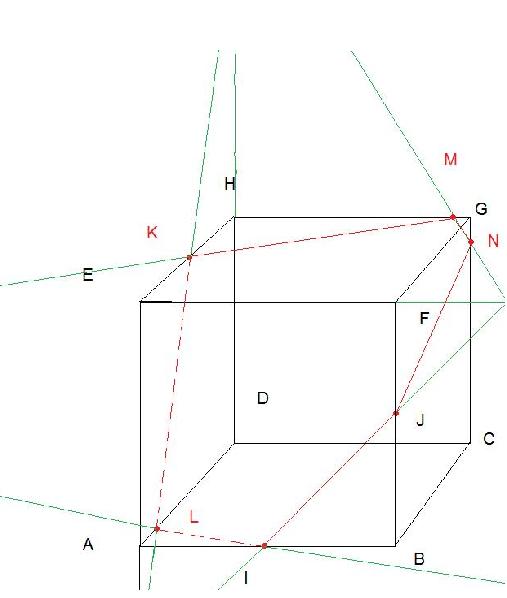
Soit ABCDEFGH un cub, ABCD étant la face du dessous et EFGH la face du dessus. Soit I le milieu de [AB], J le milieu de [FB] et K le milieu de [EH]. Construire proprement, en utilisant aucune parallèle, la coupe de ce cube par le plan (IJK).
J'ai essayé plusieurs fois mais je ne vois vraiment pas comment réaliser cette coupe, pourriez vous m'aider ? Codialement.
Tu pourrais déterminer d'abord l'intersection de plan (IJK) avec le plan de la face ABCD. Un point de cette intersection est déjà connu : c'est le point I.
Un second point serait le point d'intersection de la droite KJ et du plan ABCD. Pour le déterminer, utilise un plan auxiliaire, le plan passant par KJ et perpendiculaire au plan ABCD. Il coupe l'arête AD en un point L. Son intersection avec le plan ABCD peut être tracée . . . .
Hello,
je me permet d'intervenir. 
Ton point L est mal placé, il devrait être au milieu de [AD]. L'intersection du plan perpendiculaire à ABCD et contenant (KJ) est la droite (LB). Les droites (LB) et (KJ) se coupent en un point M, qui est le second point cherché. Donc l'intersection du plan IJK avec ABCD est selon la droite (MI)
Reste à trouver l'intersection de IJK avec EFGH.....on a déjà le point L, il faut trouver un second point N en utilisant (EF) et (IJ).
A toi de retrouver le nom des points dans la figure :
.
Annuler
connectez vous