bonsoir,

Tu fais comme pour toutes les autres fonctions, tu choisis x et tu calcules le y correspondant.

C'est ce que je pensais faire mais je n'ai pas les coordonnées de x.

Par exemple dans un exercice,je dois calculer une équation pou trouver les coordonnées x et y (celles du sommet de la prabole) ensuite je dois trouver les autres coordonnées pour pouvoir tracer le reste de la courbe mais étant donné que je n'ai pas les coordonnées de x,je ne sais pas comment faire.

hum... les coordonnées de x , cela ne veut rien dire...
x est déjà une abscisse , donc un bout des coordonnées d'un point , non?

quelles sont les données exactes de l'énoncé, peux tu le recopier?

Je me suis mal exprimée,désolée

l'exercice exacte est :

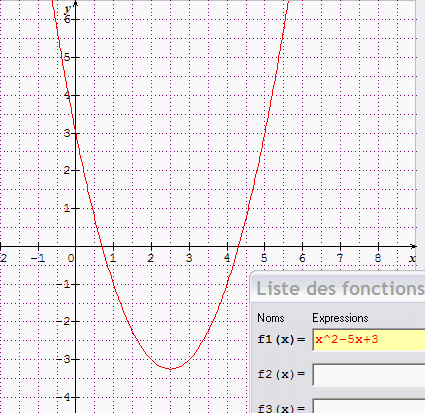
construire dans le repère orthogonal (O;i;j) la parabole (P) d'équation y= x²-5x + 3

ah oki!

Tu as dû trouver son sommet en (2,5 ; -3,25)

puis tu calcules quelques points :

x= -2=> y = (-2)²- 5*(-2) + 3 = 17 donc le point (-2; 17)
x= -1=> y = (-1)²- 5*(-1) + 3 = 9 donc le point (-1;9)
x= 0 => y = 0²- 5*0 + 3 = 3 donc le point(0;3)
x= 1 => y = 1²- 5*1 + 3 = -1 donc le point(1;-1)
x= 2 => y = 2²- 5*2 + 3 = -3 donc le point (2;-3)

etc.

Merci =)

mais dans la correction de l'exercice les résultats ne sont pas les mêmes :

la sommet de la parabole est (1,25 ; -0,125) ,

et les autres points sont :

(-1 ; 10) , (0 ; 3) , (1 ; 0) ....

ah?
tu ne t'es pas trompée dans ta formule alors?
voici ce que me donne le logiciel:

Décidément je fais que des erreurs aujourd'hui !
J'ai oublié de mettre le 2 devant le x :

2x²-5x + 3


Effectivement,ça explique la différence.
J'ai enfin compris (c'était super facile pourtant),merci beaucoup!

Dernière question,

Quel logiciel utilises-tu,s'il te plaît (ça pourrait m'être utile) ?

ah oui avec un 2 ça change les valeurs pour sûr ...

Le logiciel s'appelle SINE QUA NON , il est gratuit sur le net, il a été développé par Patrice Rabiller , un mathilien aussi .
Il te permet de tracer des fonctions, des suites, des schémas, des stats, des résolutions graphiques de syteme d'inequations etc.
Tu ne pourras plus t'en passer!

Génial!

Merci beaucoup

je t'en prie!